Регистрация Спросить otvet5GPT
karpovaarina
08.05.2020 03:55
Алгебра
Есть ответ 👍

Найдите минимальное значение функции 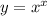y = {x}^{x}
и координаты самой низкой точки. Заранее

200
499
Посмотреть ответы 3

Ответы на вопрос:

Непатриот
Непатриот
4,6(34 оценок)

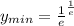
y_{min} = \frac{1}{e} ^\frac{1}{e}

Объяснение:

Здравствуйте!

Преобразуем функцию:

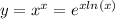
y=x^x = e^{xln(x) }

Найдем наименьшее значение функции:

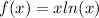
f(x) =xln(x)

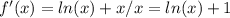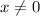
f'(x) = ln(x) +x/x = ln(x)+1 , x\neq 0

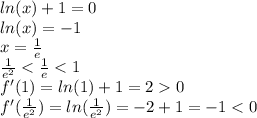
ln(x) +1 = 0\\ln(x) = -1\\x=\frac{1}{e}\\\frac{1}{e^2}

То есть 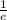\frac{1}{e } - точка минимума.

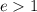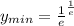
Поскольку e1 , то y_{min} = \frac{1}{e} ^\frac{1}{e}

Если вам понравился ответ, сделай его лучшим.

maschkuznetsov
maschkuznetsov
4,6(71 оценок)

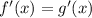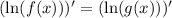По Лопиталю если f'(x) = g'(x), то (\ln(f(x)))' = (\ln(g(x)))'.

Применяем:

y = x^x

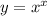
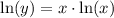
\ln(y) = x \cdot \ln(x)

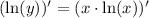
(\ln(y))' = (x \cdot \ln(x))'

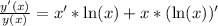
\frac{y'(x)}{y(x)} = x' * \ln(x) + x * (\ln(x))'

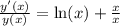
\frac{y'(x)}{y(x)} = \ln(x) + \frac{x}{x}

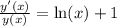
\frac{y'(x)}{y(x)} = \ln(x) + 1

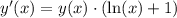
y'(x)= y(x) \cdot (\ln(x) + 1)

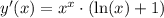
y'(x)= x^x \cdot (\ln(x) + 1)

Найдем экстремумы:

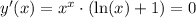
y'(x)= x^x \cdot (\ln(x) + 1) = 0

Произведение равняется 0, если один из операндов равен 0.

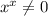x^x \neq 0, так как 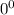0^0 - неопределённость.

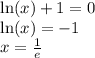
\ln(x) + 1 = 0\\\ln(x) = -1\\x = \frac{1}{e}

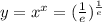
y = x^x = (\frac{1}{e})^\frac{1}{e}

simpolita
simpolita
4,5(43 оценок)
13 вроде,точно не помню

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS