Регистрация Спросить otvet5GPT
alina1749
18.11.2022 05:39
Алгебра
Есть ответ 👍

Найдите площадь области, заданной неравенством. Если можно с подробным решением

132
479
Посмотреть ответы 2

Ответы на вопрос:

Elli34
Elli34
4,6(5 оценок)

Объяснение:

|x-2|+|y+3|≤1

ОДЗ:

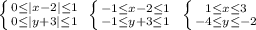
\left \{ {{0\leq |x-2|\leq1 } \atop {0\leq |y+3|\leq 1}} \ \left \{ {{-1\leq x-2\leq1 } \atop {-1\leq y+3\leq 1}} \right.\ \left \{ {{1\leq x\leq 3 } \atop {-4\leq y\leq -2 }} \right.

Сначала построим график функции |x|+|y|=1.

Первый квадрант (первая четверть):

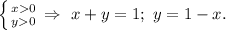
\left \{ {{x 0} \atop {y0 }} \right. \Rightarrow\ x+y=1;\ y=1-x.

Второй квадрант:

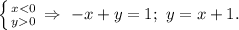
\left \{ {{x< 0} \atop y0 }} \right. \Rightarrow\ -x+y=1;\ y=x+1.

Третий квадрант:

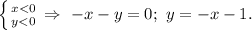
\left \{ {{x< 0} \atop {y< 0}} \right. \Rightarrow\ -x-y=0;\ y=-x-1.

Четвёртый квадрант:

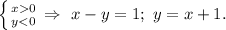
\left \{ {{x 0} \atop {y< 0}} \right. \Rightarrow\ x-y=1;\ y=x+1.

Таким образом, график выглядит следующим образом (см. рис.1)

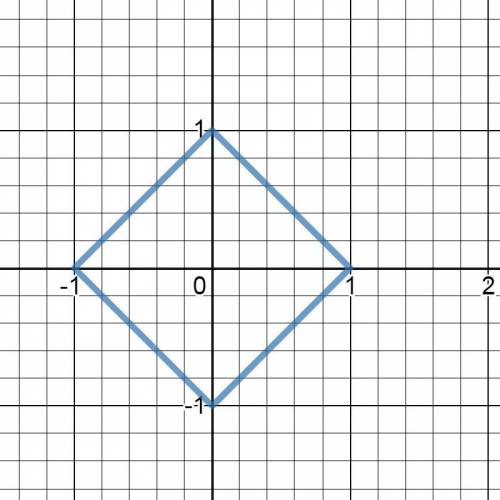
График |x-2|+|y+3|=1 - график функции |x|+|y|=1, смещённый вправо по оси ОХ на две единицы и опущенный вниз по оси ОУ на три единицы.

(см. рис 2).

Исходя из ОДЗ площадь области, заданная неравенством |x-2|+|y+3|≤1

находится внутри квадрата со стороной = √(1+1)=√2 (клетки).    ⇒

Площадь данного квадрата = (√2)²=2 (кв. клетки).

ответ: площадь области, заданная неравенством |x-2|+|y+3|≤1

равна 2 кв. клетки.


Найдите площадь области, заданной неравенством. Если можно с подробным решением
Найдите площадь области, заданной неравенством. Если можно с подробным решением
flelf
flelf
4,8(62 оценок)

по формуле и разности sin1-cos1=sin1-sin89=cos((89+1)/2)*sin((1-89)/2)=-sqrt(2)*sin(44)

1-ctg1 = (sin1-cos1)/sin1 =

-sqrt(2)*sin(44)/sin(1)

аналогично проделывая с остальными

получаем x=(-sqrt(2))^44*(sin44*sin43**sin1)/(sin1*sin2**sin44) = 2^22

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS