Регистрация Спросить otvet5GPT
Rita210606
07.11.2021 23:10
Алгебра
Есть ответ 👍

Определите количество корней уравнения |х+2|+|х-а|=а+2 в зависимости от значения параметра а​

162
356
Посмотреть ответы 2

Ответы на вопрос:

Atimofeeva876
Atimofeeva876
4,5(7 оценок)

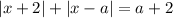
|x+2|+|x-a|=a+2

Найдем нули подмодульных выражений:

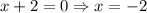
x+2=0\Rightarrow x=-2

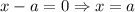
x-a=0\Rightarrow x=a

Возможны две ситуации взаимного расположения этих точек: 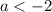a и a\geq -2.

Заметим, что первая ситуация не дает решений, так как при 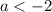a выражение в правой части уравнения 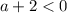a+2, но с другой стороны это выражение есть сумма модулей, которая не может быть отрицательной. Значит, при 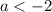a уравнение не имеет решений.

Рассмотрим ситуацию a\geq -2. Раскроем модуль при трех условиях:

1. Пусть 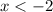x. Тогда оба модуля раскрываются со сменой знака:

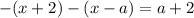
-(x+2)-(x-a)=a+2

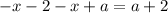
-x-2-x+a=a+2

-2x=4

x=-2

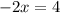
Но по условию раскрытия модулей 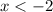x. Значит, в данном случае корней нет.

2. Пусть 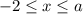-2\leq x\leq a. Тогда первый модуль раскрывается без смены знака, а второй - со сменой знака:

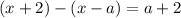
(x+2)-(x-a)=a+2

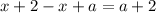
x+2-x+a=a+2

2=2

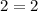
Это верное равенство. Значит, решениями являются все значения, при которых было сделано такое раскрытие модулей:

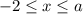
-2\leq x\leq a

3. Пусть 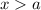xa. Тогда оба модуля раскрываются без смены знака:

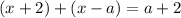
(x+2)+(x-a)=a+2

x+2+x-a=a+2

2x=2a

x=a

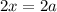
Но по условию раскрытия модулей 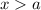xa. Значит, в данном случае корней нет.

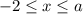Таким образом, корни имеются только при условии a\geq -2. Они определяются соотношением -2\leq x\leq a.

Выделив условие 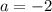a=-2 как частный случай, можно записать ответ.

при 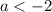a: нет корней

при 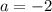a=-2: один корень x=-2

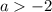при a-2: бесконечное множество корней: x\in[-2;\ a]

dsassaraf
dsassaraf
4,5(45 оценок)
Пусть r=5 радиус шара, h=4расстояние от центра шара до сечения, r радиус сечения. найдем радиус сечения по теореме пифагора r^2=r^2-h^2 r=√(25-16)=√9=3 тогда площадь сечения равна s=πr^2=9π

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS