01.01.2021 02:49

Есть ответ 👍

Найти восемнадцатый член арифметической прогрессии, если первый и одиннадцатый ее члены - натуральные числа, а сумма первых четырнадцати членов равна 77.

247

426

Посмотреть ответы 2

Ответы на вопрос:

morozu020

Математика

4,8(98 оценок)

Распишем сумму четырнадцати членов:

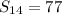
$S_{14}=77$

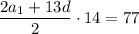
$\dfrac{2a_1+13d}{2} \cdot 14=77$

Упростим соотношение:

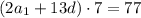
$(2a_1+13d)\cdot 7=77$

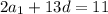
2a_1+13d=11

Выразим разность:

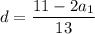
$d=\dfrac{11-2a_1}{13}$

Запишем выражение для одиннадцатого член:

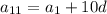
$a_{11}=a_1+10d$

Подставим выражение для d:

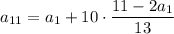
$a_{11}=a_1+10\cdot\dfrac{11-2a_1}{13}$

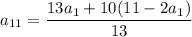
$a_{11}=\dfrac{13a_1+10(11-2a_1)}{13}$

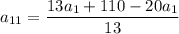
$a_{11}=\dfrac{13a_1+110-20a_1}{13}$

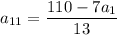
$a_{11}=\dfrac{110-7a_1}{13}$

Проверим, при каких натуральных 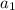a_1 значение 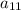$a_{11}$ также будет натуральным.

Подставляя натуральные 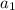a_1 в выражение для числителя найдем те значения, при которых числитель кратен 13:

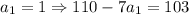
$a_1=1\Rightarrow 110-7a_1=103$

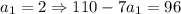
$a_1=2\Rightarrow 110-7a_1=96$

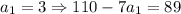
$a_1=3\Rightarrow 110-7a_1=89$

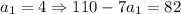
$a_1=4\Rightarrow 110-7a_1=82$

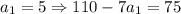
$a_1=5\Rightarrow 110-7a_1=75$

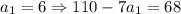
$a_1=6\Rightarrow 110-7a_1=68$

$a_1=7\Rightarrow 110-7a_1=61$

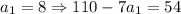
$a_1=8\Rightarrow 110-7a_1=54$

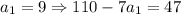
$a_1=9\Rightarrow 110-7a_1=47$

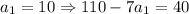
$a_1=10\Rightarrow 110-7a_1=40$

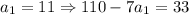
$a_1=11\Rightarrow 110-7a_1=33$

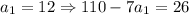$a_1=12\Rightarrow 110-7a_1=26$ - 26 кратно 13

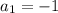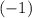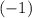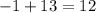Можно было заметить, что (110-7a_1) делится на 13 при a_1=-1 , но так как (-1) - не натуральное число, то искать необходимо было натуральное число, равное (-1) по модулю 13. Наименьшее такое число -1+13=12 .

Таким образом, 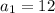a_1=12 .

Проверим, что одиннадцатый член является натуральным числом:

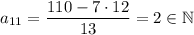
$a_{11}=\dfrac{110-7\cdot12}{13}=2\in\mathbb{N}$

Найдем разность:

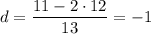
$d=\dfrac{11-2\cdot12}{13}=-1$

Найдем восемнадцатый член:

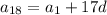
$a_{18}=a_1+17d$

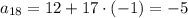
$a_{18}=12+17\cdot(-1)=-5$

ответ: -5

basik100grn

Математика

4,8(54 оценок)

с g dz .r u спиши там класс выбираешь и предмет, потом учебник ищишь

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.