stasamaca

28.05.2021 08:36

Геометрия

Есть ответ 👍

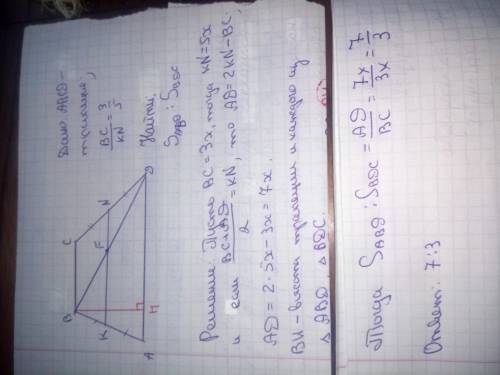
решить Отношение меньшего основания трапеции к средней линии 3:5.В каком отношении делит диагональ этой трапеции ее площадь.

191

319

Посмотреть ответы 3

Ответы на вопрос:

11nastyaaaaa11

Геометрия

4,4(49 оценок)

Пусть a - меньшее основание, b - большее основание, m - средняя линия. Тогда по условию:

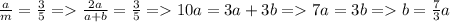
$\frac{a}{m} = \frac{3}{5} = \frac{2a}{a+b} = \frac{3}{5} = 10a = 3a+3b = 7a = 3b = b = \frac{7}{3}a$

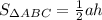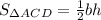Теперь рассмотрим ΔABC. Его площадь $S_{\Delta ABC} = \frac{1}{2} ah$ , где h - это высота трапеции. Аналогично для ΔACD: $S_{\Delta ACD} = \frac{1}{2}bh$ .

Тогда отношение площадей равно:

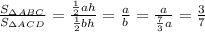
$\frac{S_{\Delta ABC}}{S_{\Delta ACD}} = \frac{\frac{1}{2}ah }{\frac{1}{2}bh } = \frac{a}{b} = \frac{a}{\frac{7}{3}a } = \frac{3}{7}$

ответ: $\frac{3}{7}$

Amdrek

Геометрия

4,4(18 оценок)

7:3

Решение задания прилагаю

решить Отношение меньшего основания трапеции к средней линии 3:5.В каком отношении делит диагональ э

Анжела921

Геометрия

4,8(56 оценок)

АВСД - равнобокая трапеция, АВ=СД, ВС=6 см, ∠АВС=120° , ∠САД=30°. Найти АС.

Пошаговое объяснение:

Так как ∠АВС=120°, то ∠ВАД=180°-120°=60° ,

∠САД=30° ⇒ ∠ВАС=∠ВАД-∠САД=60°-30°=30° .

диагональ АС - биссектриса ∠А .

∠АСВ=∠САД=30° как внутренние накрест лежащие при АД || ВC и секущей АС ⇒ ΔАВС - равнобедренный , т.к. ∠ВАС=∠АСВ .

значитит, АВ=АС=6 см .

Опустим перпендикуляры на основание АД из вершин В и С: ВН⊥АС , СМ⊥АД , получим прямоугольник ВСМН и два треугольника АВН и СМД .

Рассмотрим ΔАВН: ∠ВНА=90°, ∠ВАН=∠ВАД=60° , АВ=6 см ⇒

∠АВН=90°-80°=30°

Против угла в 30° лежит катет, равный половине гипотенузы ⇒ АН=6:2=3 см.

Так как ΔАВН=ΔСМД (по гипотенузе АВ=СД и острому углу ∠ВАД=∠АДС), то МД=АН=3 см.

НМ=ВС=6 см

АД=АН+НМ+МД=3+6+3=12 см.

Объяснение:

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.