Sin4x+sin7x=cos4x+cos7x В ответе запишите наибольший отрицательный корень уравнения (в градусах) умноженный на 11

128

300

Посмотреть ответы 2

Ответы на вопрос:

hdhushehsuu

Математика

4,7(10 оценок)

-270

Пошаговое объяснение:

Воспользуемся формулами суммы синусов и суммы косинусов:

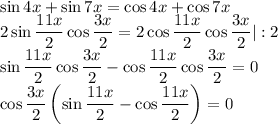
$\sin{4x}+\sin{7x}=\cos{4x}+\cos{7x}\\2\sin{\dfrac{11x}{2}}\cos{\dfrac{3x}{2}}=2\cos{\dfrac{11x}{2}}\cos{\dfrac{3x}{2}}|:2\\\sin{\dfrac{11x}{2}}\cos{\dfrac{3x}{2}}-\cos{\dfrac{11x}{2}}\cos{\dfrac{3x}{2}}=0\\\cos{\dfrac{3x}{2}}\left(\sin{\dfrac{11x}{2}}-\cos{\dfrac{11x}{2}}\right)=0$

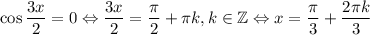$\cos{\dfrac{3x}{2}}=0\Leftrightarrow\dfrac{3x}{2}=\dfrac{\pi}{2}+\pi k, k\in\mathbb{Z}\Leftrightarrow x=\dfrac{\pi}{3}+\dfrac{2\pi k}{3}$ . При k = 0 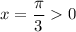$x=\dfrac{\pi}{3}0$ , при k = -1 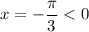$x=-\dfrac{\pi}{3}$ — наибольший отрицательный корень в данной серии.

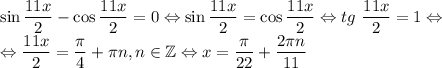
$\sin{\dfrac{11x}{2}}-\cos{\dfrac{11x}{2}}=0\Leftrightarrow\sin{\dfrac{11x}{2}}=\cos{\dfrac{11x}{2}}\Leftrightarrow tg\ \dfrac{11x}{2}=1\Leftrightarrow\\ \Leftrightarrow \dfrac{11x}{2}=\dfrac{\pi}{4}+\pi n, n\in\mathbb{Z}\Leftrightarrow x=\dfrac{\pi}{22}+\dfrac{2\pi n}{11}$

При n = 0 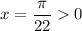$x=\dfrac{\pi}{22}0$ , при n = -1 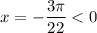$x=-\dfrac{3\pi}{22}$ — наибольший отрицательный корень в данной серии.

Так как 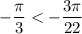$-\dfrac{\pi}{3}$ , наибольший отрицательный корень уравнения — 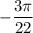$-\dfrac{3\pi}{22}$ . В ответ запишем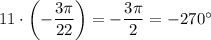 $11\cdot\left(-\dfrac{3\pi}{22}\right)=-\dfrac{3\pi}{2}=-270^{\circ}$

omy00god

Математика

4,8(30 оценок)

Первый угадал 16*1/4=4 песни остальные двое угадали 16-4=12 песен каждый из них двоих по 12/2=6 песен.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.