Регистрация Спросить otvet5GPT
Машkа
19.06.2023 04:47
Алгебра
Есть ответ 👍

Решите уравнение с решением

273
386
Посмотреть ответы 2

Ответы на вопрос:

20Lorans03
20Lorans03
4,5(57 оценок)

x=1

Объяснение:

рассмотрим функцию:

f(x)=\frac{x^2}{4}+\frac{3}{4} -\sqrt[4]{2x-1}

2x-1≥0 ⇔ x≥0.5

Её область определения: D(f)=[0.5;+∞)

Исследуем ее с производной:

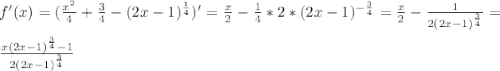
f'(x)=(\frac{x^2}{4}+\frac{3}{4} -(2x-1)^\frac{1}{4} )'=\frac{x}{2} -\frac{1}{4}*2*(2x-1)^{-\frac{3}{4} } =\frac{x}{2} -\frac{1}{2(2x-1)^{\frac{3}{4} }} = \\ \\ \frac{x(2x-1)^{\frac{3}{4} }-1}{2(2x-1)^{\frac{3}{4} }}

Находим нули числителя:

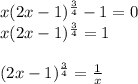
x(2x-1)^{\frac{3}{4} }-1=0 \\ x(2x-1)^{\frac{3}{4} }=1 \\ \\ (2x-1)^{\frac{3}{4} }=\frac{1}{x}

Замечаем, что слева стоит возрастающая функция, справа - убывающая. Поэтому если и есть корень, то он единственный!

Не трудно догадаться, что корнем будет x=1

Теперь находим нули знаменателя:

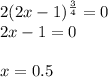
2(2x-1)^{\frac{3}{4} }=0 \\ 2x-1=0 \\ \\ x=0.5

метод интервалов с учетом D(f)

(0,5)---[1]---->ₓ

С пробных точек узнаем знаки промежутков и получаем:

(0,5)---[1]+++>ₓ

На интервале (0,5;1) производная отрицательна, значит функция убывает.

На интервале (1;+∞) производная положительна, значит функция возрастает

Таким образом x=1 - точка минимума и в том числе точка наименьшего значения функции

f(1)=\frac{1}{4}+\frac{3}{4}-\sqrt[4]{2*1-1}=0

f(1)=0 - минимум и наименьшее значение функции

Таким образом мы выяснили, что f(x)≥0 при всех допустимых x, а равенство f(x)=0 достигается только в точке x=1 (в точке минимума)

vastgfy
vastgfy
4,8(18 оценок)
(x-6)(5^(x-6)-25)< 0 x-6=0 5^(x-6)-25> 0 x-6> 0 5^(x-6)-25< 0 x< 6 x> 8 x> 6 x< 8 x∈(6; 8)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS