Ответы на вопрос:
Рассмотрим выражение 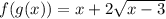 . Так как под знаком корня стоит выражение
. Так как под знаком корня стоит выражение 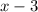 , то попробуем получить такое же выражение не под знаком корня:
, то попробуем получить такое же выражение не под знаком корня:
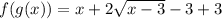
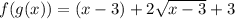
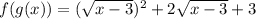
Теперь можно сказать, что такая функция зависит от выражения 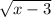 . Но функция
. Но функция 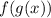 зависит от
зависит от 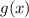 . Значит, мы получили выражение для
. Значит, мы получили выражение для 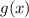 :
:
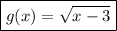
Таким образом:
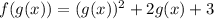
Переобозначив, получим выражение для 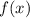 :
:
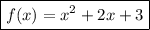
2sin²x - √3sin2x =0; - 2sin²x - √3*2sinx *cosx=0; -2sinx(sinx -√3cosx) = 0 ; [ sinx = 0 ; sinx -√3cosx =0 ; a) sinx = 0 ⇒ x = π*k , k∈z ; . b) sinx -√3cosx =0 ⇔tqx =√3 ⇒x =π/3 + π*k , k∈z. ответ : π*k ; π/3 + π*k , k∈z. ******************************************** 2sin²x = 1 +cosx ; - (1 -2sin²x) = cosx ; - cos2x = cosx ; cos2x +cosx =0 ; * * * * * cosα +cosβ =2cos(α+β)/2* cos(α - β)/2 * * * * * 2cos3x/2*cosx/2 =0 ; cos3x/2 = 0 ⇒3x/2 =π/2+π*k , k∈z⇔x = π/3+2π/3*k , k∈z ; cosx/2 =0⇒x/2 =π/2+π*k , k∈z⇔x = π+2π*k ,k∈z. ответ : π/3+2π/3*k ; π+2π*k , k∈z.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Дайте названия процессвязанных с движением литосферных плит 1) 2) 3) [3]...
 Lorosa09.01.2022 00:52
Lorosa09.01.2022 00:52 -
Найдите периметр фигуры. ответ запишите в виде многочлена стандартного...
 mariya26046418.11.2020 00:14
mariya26046418.11.2020 00:14 -
Көбейткішке жіктеңіз: 5х/2+5ax+7a+7x:...
 Kiralex7113.10.2020 03:13
Kiralex7113.10.2020 03:13 -
Угол между меньшей диагональю АС ромба АВСД и стороной АВ равен 63°.Найдите...
 apzjxmskaposjxhdh26.01.2023 02:50
apzjxmskaposjxhdh26.01.2023 02:50 -
Среди данных одночленов выберите те, степень которых равна 9: 1) −8a7...
 YaKrevedko109.12.2020 20:23
YaKrevedko109.12.2020 20:23 -
(1 1/3) в степені -5 помножити (9/16) в степені -3...
 bastovayasofia19.12.2021 09:38
bastovayasofia19.12.2021 09:38 -
Y= (a +1)x + a −1 пересекает ось абсцисс в точке с координатами (-2; 0)...
 devoshka200615.12.2021 22:00
devoshka200615.12.2021 22:00 -
Розкладіть на множники многочлен: х в другому степені + 2ху+у в другому...
 Yarick200520.06.2022 22:15
Yarick200520.06.2022 22:15 -
Решите . нужно! ) 4x²·x³-2x⁶: x 3(ab)²·(-4)(3a)² \sqrt{16}: \sqrt{ \frac{1}{9}...
 pudish22.06.2020 05:23
pudish22.06.2020 05:23 -
Известно,что график функции y=k/x проходит через точку a(-3; 6). найдите...
 calusiker13.03.2023 02:24
calusiker13.03.2023 02:24

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

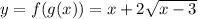 Указать функции
Указать функции