Регистрация Спросить otvet5GPT
20031003veronika
09.02.2021 18:04
Алгебра
Есть ответ 👍

До кожного виразу доберіть тотожно рівний йому вираз. (щоб було легше писати відповідь можете просто написати цифру і до неї відповідну букву, Наприклад: 1... , 2... , 3...) До ть будь ласка.​

297
497
Посмотреть ответы 3

Ответы на вопрос:

yaku06nastyaozq1r7
yaku06nastyaozq1r7
4,5(64 оценок)

№1

(а-8)(а+8)=а²-8²=а²-64;  - Д) разность квадратов

№2

(а-8)²=а²-16а+64;  -  А) квадрат разности

№3

(а-4)(а²+4а+16)=а³-64;  -  Г) разность кубов. (а³-в³)=(а-в)(а²+ав+в²)

№4

(а-4)(а-16)  -  Д) разложение квадратного 3-х члена на множители.

ах²+вх+с=а(х-х1)(х-х2); х1 и х2 - корни кв. 3-х члена

а²-20а+64=0

D=20²-4*1*64=400-256=144=12²

а1=(20+12)/2=16;  а2=(20-12)/2=4

а²-20а+64=(а-16)(а-4)

----------------------------------------

Можно легче. D/4=(b/2)²-ac=100-64=36=6²

a1=10+6=16;  a2=10-6=4

ИЛИ по т. Виета

а1*а2=64;   а1+а2=20; а1=16; а2=4.

helpmepls1234566
helpmepls1234566
4,6(85 оценок)

А) (а²-16а+64)=(а-8)²  это 2)

Б)а³+64=(а+4)(а²- 4а+ 16) ответа не нашел в предложенных

В) а²-64=(а-8)(а+8) это 1)

Г) а³-64=(а-4)(а²+ 4а+ 16) это 3)

Д) а²-20а+64 =(а-4)(а-16) это 4)

yarrik00yaroslavchik
yarrik00yaroslavchik
4,5(80 оценок)

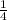
\frac{1}{4}

Объяснение:

Сумма кубов натуральных чисел от 1 до n равна 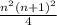\frac{n^{2} (n+1)^{2} }{4}

Формулы для суммы степеней натуральных чисел получаются следующим Покажем это  на примере суммы квадратов

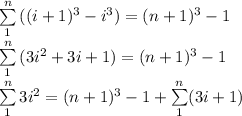
\sum\limits^n_1 {((i+1)^{3}-i^{3})} = (n+1)^{3}-1\\\sum\limits^n_1 {(3i^{2}+3i+1)}=(n+1)^{3}-1\\\sum\limits^n_1 {3i^{2}}=(n+1)^{3}-1+\sum\limits^n_1(3i+1)

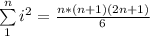
\sum\limits^n_1 {i^{2}}=\frac{n*(n+1)(2n+1)}{6}

Для вывода формулы суммы кубов используется следующее соотношение

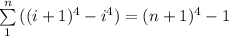
\sum\limits^n_1 {((i+1)^{4}-i^{4})} = (n+1)^{4}-1

Раскрываем скобки под знаком суммы и выражаем сумму кубов через сумму второй, первой и нулевой степени i.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS