olegyagubov01

09.06.2022 16:31

Математика

Есть ответ 👍

второй раз публикую вопрос, хотя бы посоветуйте что делать? Очень нужно составить формулу. P1 = изначальная сумма инвестирования = 100р.;
P2 = сумма довложений за каждый период = 5р;
i = процент доходности за период = 20%;
n = кол-во периодов = 3

Задача: Мы инвестировали 100р. под 20% и в конце каждого периода добавляем 5р. Периодов всего 3.

Пример расчета:
P1(1+20/100)+P2=S1

1) 100(1+20/100)+5=125
2) 125(1+20/100)+5=155
3) 155(1+20/100)+5=191

ВОПРОС: есть ли формула для такого расчета исходя из количества периодов? Чтобы не считать за каждый отдельно, например периодов может быть не 3, а 10 и т.д.

* В файле прикрепил пример такого расчета на калькуляторе.

119

278

Посмотреть ответы 2

Ответы на вопрос:

oksaniana

Математика

4,8(26 оценок)

проверяй:)

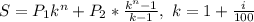
$S=P_1k^n+P_2*\frac{k^n-1}{k-1}, \ k=1+\frac{i}{100}$

Пошаговое объяснение:

для упрощения обозначим коэффициент 1+(i/100)=k

исходя из примера расчета, можно объединить в один пример за период 3:

то есть,

((100*1.2+5)*1.2+5)*1.2+5=191

Тогда в общем виде будет:

((P₁k+P₂)k+P₂)k+P₂...=S

Раскрываем скобки

(P₁k² +P₂k+P₂)k+P₂...=S

P₁k³+P₂k²+P₂k+P₂...=S

Замечаем явную закономерность, тогда для периода n лучше записать так:

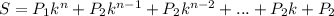
$S=P_1k^n+P_2k^{n-1}+P_2k^{n-2}+...+P_2k+P_2$

Вынесем P₂ за скобки

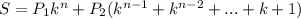
$S=P_1k^n+P_2(k^{n-1}+k^{n-2}+...+k+1)$

А теперь смотрим, что же у нас такое в скобках?

Если не очень понятно, можно записать справа налево:

1+k+k²+k³+...+kⁿ⁻²+kⁿ⁻¹ - это сумма геометрической прогрессии, у которой b₁=1; q=k; и содержит она как раз n слагаемых.

Для нее есть формула:

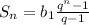
$S_n=b_1\frac{q^n-1}{q-1}$

Тогда в нашем случае:

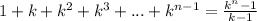
$1+k+k^2+k^3+...+k^{n-1}=\frac{k^n-1}{k-1}$

Подставляем в исходную формулу:

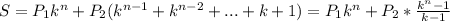
$S=P_1k^n+P_2(k^{n-1}+k^{n-2}+...+k+1)=P_1k^n+P_2*\frac{k^n-1}{k-1}$

P.S.

Выражая другие значения можно получить следующие формулы:

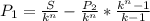
$P_1=\frac{S}{k^n}- \frac{P_2}{k^n}*\frac{k^n-1}{k-1}$

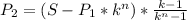
$P_2=(S-P_1*k^n)*\frac{k-1}{k^n-1}$

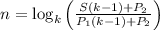
$n=\log_k\left(\frac{S(k-1)+P_2}{P_1(k-1)+P_2} \right)$

Чтобы выразить i, надо сначала выразить k, что в явном виде невозможно. При определенных значениях остальных параметров, подставляем всё в уравнение

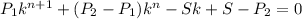
$P_1k^{n+1}+(P_2-P_1)k^n-Sk+S-P_2=0$

и находим k, а дальше:

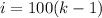
i=100(k-1)

rrv1803

Математика

4,4(12 оценок)

F(x)=x^3-12x-1 на отрезке [1; 3]f'(x)=3x²-12, f'(x)=3x²-12=0,3(x²-4)=3(x-2)(x+2)=0 x₁=-2,x₂=2 проверяем значения функции в т.х=1,х=2 и х=3 f(1)=1³-12-1=-12 f(2)=2³-12·2-1=8-24-1=-17 f(3)=3³-12·3-1=27-24-1=2 функция достигает максимума в т.х=3 и он равен 2

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.