Регистрация Спросить otvet5GPT
kotik53Tv
19.05.2023 09:58
Алгебра
Есть ответ 👍

Найдите наибольшую площадь трапеции, если три ее стороны равны а

285
347
Посмотреть ответы 2

Ответы на вопрос:

olinka6
olinka6
4,7(50 оценок)

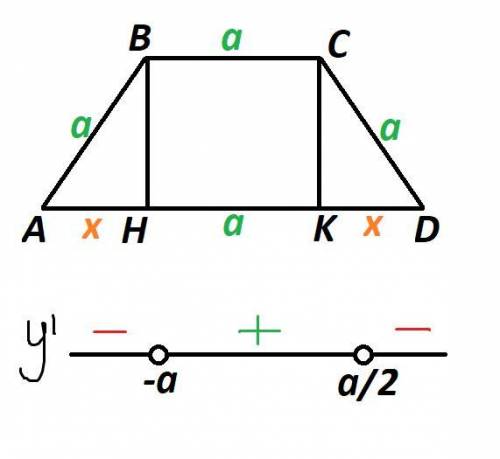
Рассмотрим трапецию ABCD.

Основания трапеции не могут иметь одинаковую длину, так как в противном случае это будет параллелограмм. Значит, одно из оснований  BC и две боковые стороны AB и CD равны по а. Заметим, что рассматриваемая трапеция равнобедренная.

Проведем высоты BH и CK. Тогда, HK=а.

Обозначим AH=KD=х.

Высоту трапеции найдем по теореме Пифагора:

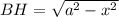
BH=\sqrt{a^2-x^2}

Запишем выражение для площади трапеции:

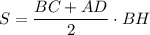
S=\dfrac{BC+AD}{2}\cdot BH

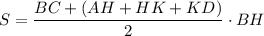
S=\dfrac{BC+(AH+HK+KD)}{2}\cdot BH

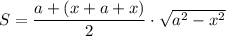
S=\dfrac{a+(x+a+x)}{2}\cdot \sqrt{a^2-x^2}

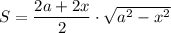
S=\dfrac{2a+2x}{2}\cdot \sqrt{a^2-x^2}

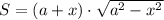
S= (a+x)\cdot\sqrt{a^2-x^2}

Исследуем на экстремумы функцию S. Найдем производную:

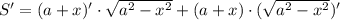
S'= (a+x)'\cdot\sqrt{a^2-x^2}+(a+x)\cdot(\sqrt{a^2-x^2})'

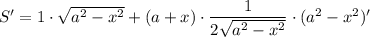
S'=1\cdot\sqrt{a^2-x^2}+(a+x)\cdot\dfrac{1}{2\sqrt{a^2-x^2}} \cdot(a^2-x^2)'

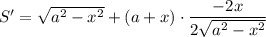
S'=\sqrt{a^2-x^2}+(a+x)\cdot\dfrac{-2x}{2\sqrt{a^2-x^2}}

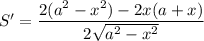
S'=\dfrac{2(a^2-x^2)-2x(a+x)}{2\sqrt{a^2-x^2}}

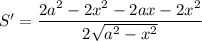
S'=\dfrac{2a^2-2x^2-2ax-2x^2}{2\sqrt{a^2-x^2}}

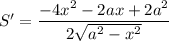
S'=\dfrac{-4x^2-2ax+2a^2}{2\sqrt{a^2-x^2}}

Найдем нули производной:

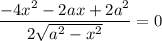
\dfrac{-4x^2-2ax+2a^2}{2\sqrt{a^2-x^2}}=0

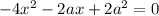
-4x^2-2ax+2a^2=0

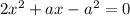
2x^2+ax-a^2=0

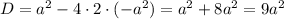
D=a^2-4\cdot2\cdot(-a^2)=a^2+8a^2=9a^2

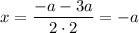
x=\dfrac{-a-3a}{2\cdot2}=-a

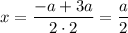
x=\dfrac{-a+3a}{2\cdot2}=\dfrac{a}{2}

При переходе через точку 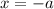x=-a производная меняет знак с минуса на плюс, значит это точка минимума.

При переходе через точку 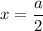x=\dfrac{a}{2} производная меняет знак с плюса на минус, значит это точка максимума.

Таким образом, наибольшую площадь трапеция имеет при 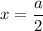x=\dfrac{a}{2}. Эта площадь равна:

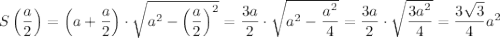
S\left(\dfrac{a}{2}\right)= \left(a+\dfrac{a}{2}\right)\cdot\sqrt{a^2-\left(\dfrac{a}{2}\right)^2}= \dfrac{3a}{2}\cdot\sqrt{a^2-\dfrac{a^2}{4}}=\dfrac{3a}{2}\cdot\sqrt{\dfrac{3a^2}{4}}=\dfrac{3\sqrt{3} }{4}a^2

ответ: 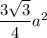\dfrac{3\sqrt{3} }{4}a^2


Найдите наибольшую площадь трапеции, если три ее стороны равны а
Anutka15Love
Anutka15Love
4,8(69 оценок)
Незнаю, может будет предпоследняя, извини

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS