Регистрация Спросить otvet5GPT
Поглит
27.07.2022 20:18
Алгебра
Есть ответ 👍

ТЕ, КТО РАЗБИРАЕТСЯ В МАТЕМАТИКЕ! ОБЪЯСНИТЕ, УМОЛЯЮ! Дано тригонометрическое уравнение: sin2x+2sinx=1+cosx

Мне нужно найти корни, принадлежащие отрезку [-4; -3].

Я решила уравнение, но не понимаю как отобрать корни!! Ведь мне даны не градусы и не радианы, а обычные числа. КАК ЭТО ВООБЩЕ ПОНЯТЬ???? ОБЪЯСНИТЕ

291
293
Посмотреть ответы 2

Ответы на вопрос:

Салатикус
Салатикус
4,8(18 оценок)

sin2x + 2sinx = 1 + cosx\\2sinxcosx+2sinx=1+cosx\\2sinx(1+cosx) = 1 + cosx\\(2sinx-1)(1+cosx) = 0\\sinx = \frac{1}{2} = x = (-1)^n\frac{\pi}{6} + \pi n, n \in Z\\ cosx = -1 = x = \pi + 2\pi m, m \in Z\\x \in [-4;-3]\\-4 < (-1)^n\frac{\pi}{6} + \pi n < -3\\-24 < (-1)^n\pi+6\pi n < -18\\

Подставляем n = 0 - неравенство не выполнено. n = 1 - неравенство не выполнено. Следовательно, при n ≥ 0 решений не будет, т.к.  (-1)^n + 6n - функция возрастающая.

Пусть n = -1, тогда выражение 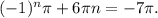(-1)^n\pi + 6\pi n = -7\pi. Так как 3.14 < π < 3.15, то

-22.05  < -7π < -21.98. Очевидно, оно попадает на промежуток (-24; -18). Значит, при n = -1 решение есть на данном отрезке. Подставим n = -1 в серию корней:

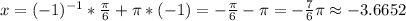
x = (-1)^{-1}*\frac{\pi}{6} + \pi * (-1) = -\frac{\pi}{6} - \pi = -\frac{7}{6}\pi \approx -3.6652

Такими же рассуждениями приходим к тому, что n ≤ -2 так же не являются решениями.

Теперь рассмотрим вторую серию корней:

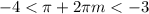
-4 < \pi + 2\pi m < -3\\

Тут совсем все просто: при m = 0, очевидно, неравенство не выполнено. При m = 1 так же. Так как выражение 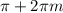\pi + 2\pi m при возрастании m увеличивается, то и m ≥ 2 также не подходят.

Пусть m = -1, тогда:

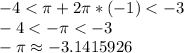
-4 < \pi + 2\pi * (-1) < -3\\-4 < -\pi < -3\\-\pi \approx -3.1415926

Очевидно, что это так. Подставляя m = -2 понимаем, что число меньше -4.

Вопросы ниже в комменты.

ответ: 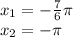x_1 = -\frac{7}{6} \pi\\x_2 = -\pi

Sahfejdie24810572947
Sahfejdie24810572947
4,6(47 оценок)
4х²-8х+3 = 4х²-2×2х×2+4-1 = (2х-2)²-1

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS