решить Найти сумму корней уравнения cos3x⋅cos6x=cos4x⋅cos7x на промежутке [π/3;π/2]

274

410

Посмотреть ответы 2

Ответы на вопрос:

lyubaykind

Математика

4,7(31 оценок)

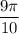
$\dfrac{9\pi}{10}$

Пошаговое объяснение:

Воспользуемся формулой произведения косинусов: 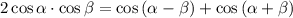$2\cos{\alpha}\cdot\cos{\beta}=\cos{(\alpha -\beta)}+\cos{(\alpha +\beta)}$

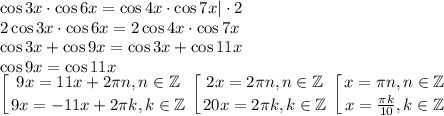
$\cos{3x}\cdot\cos{6x}=\cos{4x}\cdot\cos{7x}|\cdot 2\\2\cos{3x}\cdot\cos{6x}=2\cos{4x}\cdot\cos{7x}\\\cos{3x}+\cos{9x}=\cos{3x}+\cos{11x}\\\cos{9x}=\cos{11x}\\\displaystyle \left [ {{9x=11x+2\pi n, n\in\mathbb{Z}} \atop {9x=-11x+2\pi k, k\in\mathbb{Z}}} \right. \left [ {{2x=2\pi n, n\in\mathbb{Z}} \atop {20x=2\pi k, k\in\mathbb{Z}}} \right. \left [ {{x=\pi n, n\in\mathbb{Z}} \atop {x=\frac{\pi k}{10}, k\in\mathbb{Z}}} \right.$

В первой серии корней на указанном промежутке нет: при n = 0 x = 0 < π/3, при n = 1 x = π > π/2.

Отберём корни из второй серии:

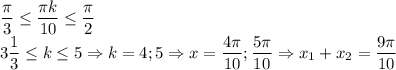
$\dfrac{\pi}{3}\leq \dfrac{\pi k}{10}\leq \dfrac{\pi}{2}\\3\dfrac{1}{3}\leq k\leq 5\Rightarrow k=4;5\Rightarrow x=\dfrac{4\pi}{10};\dfrac{5\pi}{10}\Rightarrow x_1+x_2=\dfrac{9\pi}{10}$

angelina2334e35r5

Математика

4,8(12 оценок)

240 / 8 - 3 / 2 + 561 / 17 + 66 / 11=? расставим скобки для наглядности: (240 / 8) - (3 / 2) + (561 / 17) + (66 / 11) 240 / 8=30 3/2=1,5 561 / 17=33 66 / 11=6 30-1,5+33+6=67,5 ответ: 67,5

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.