Ответы на вопрос:
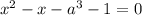 .
.
Уравнение - квадратное вида 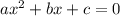 . Здесь
. Здесь 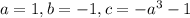 .
.
Чтобы уравнение имело корни нужно чтобы дискриминант был неотрицательным:  .
.
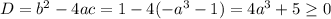
![4a^3\geq -5;\\\\a^3\geq -\frac{5}{4};\\\\ a\geq \sqrt[3]{\frac{-5}{4} } =-\frac{\sqrt[3]{5}\sqrt[3]{2}}{\sqrt[3]{8}}=-\frac{\sqrt[3]{10}}{2}](/tpl/images/3782/0065/7ecfd.png)
Если дискриминант равен 0 ( при ![a=-\frac{\sqrt[3]{10} }{2}](/tpl/images/3782/0065/650cc.png) ), то уравнение имеет единственное решение
), то уравнение имеет единственное решение 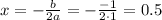 . Поскольку 0,5 > 0, значение параметра
. Поскольку 0,5 > 0, значение параметра ![a=-\frac{\sqrt[3]{10} }{2}](/tpl/images/3782/0065/650cc.png) пойдет в ответ.
пойдет в ответ.
Если дискриминант положителен (при ![a-\frac{\sqrt[3]{10} }{2}](/tpl/images/3782/0065/a9de6.png) ), то уравнение имеет 2 корня. Расписывать их необязательно.
), то уравнение имеет 2 корня. Расписывать их необязательно.
Чтобы ровно один корень из двух был положителен необходимо и достаточно того, чтобы произведение корней было отрицательным.
Если 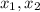 - корни уравнения, то по теореме Виета
- корни уравнения, то по теореме Виета 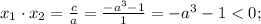
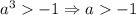
Нужно учесть, что должно также выполняться условие ![a-\frac{\sqrt[3]{10} }{2}](/tpl/images/3782/0065/a9de6.png) , так как в противном случае вещественных корней уравнение иметь не будет. Промежуток
, так как в противном случае вещественных корней уравнение иметь не будет. Промежуток ![(-\frac{\sqrt[3]{10} }{2}; +\infty)](/tpl/images/3782/0065/921c4.png) включает в себя промежуток
включает в себя промежуток 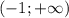 , поэтому все значения параметра
, поэтому все значения параметра 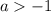 также пойдут в ответ.
также пойдут в ответ.
ОТВЕТ можно записать в двух видах: при ![a=-\frac{\sqrt[3]{10}}{2}](/tpl/images/3782/0065/f1e21.png) и
и 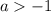 ; при
; при 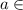 {
{![-\frac{\sqrt[3]{10}}{2}](/tpl/images/3782/0065/9e7d0.png) }
}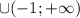 .
.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Разложи на множители: 10z^2-20zy+10y^2 Известно,что один множитель разложения...
 Natalii201708.03.2022 07:50
Natalii201708.03.2022 07:50 -
Преобразуй в многочлен −2(0,2p−t)2 (во 2-ой степени плз...
 ВероникаКарпова15.06.2022 01:28
ВероникаКарпова15.06.2022 01:28 -
Чем отличается формула каадрата суммы от формулы куба суммы сами формулы...
 knoposhka12325.06.2021 23:20
knoposhka12325.06.2021 23:20 -
Решите неравенство: 7/x-x/7 больше 0...
 Гелакси2708.10.2022 15:00
Гелакси2708.10.2022 15:00 -
Какие выражения равны данному выражению 2p+2e? 1. (p+e)×2 2. 2(-p-e)...
 StenxgenS15.09.2020 16:00
StenxgenS15.09.2020 16:00 -
Монету підкинули 150 разів. У результаті цього експерименту 81 разів...
 Барбоси03.08.2020 15:00
Барбоси03.08.2020 15:00 -
Функціям = f(x) визначена на всій числовій прямій і є періодичною з...
 2018309.05.2023 21:03
2018309.05.2023 21:03 -
Решите уравнение -6/x^2-9-x+1/x-3=1/x+3...
 natalavorik22.07.2020 01:32
natalavorik22.07.2020 01:32 -
Pomogite pojaluista s 4 zadaniem. nujno postroit eti grafiki. srochno...
 korgavinaolga02.03.2021 14:14
korgavinaolga02.03.2021 14:14 -
Постройте график функции y=-x^2-6x-5 и укажите: 1) область определения...
 Indira676703.11.2020 18:28
Indira676703.11.2020 18:28

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
