Більший кут трикутника дорівнює 120°. Під яким кутом видно більшу сторону цього трикутника з точки перетину бісектрис гострих кутів трикутника?

127

474

Посмотреть ответы 2

Ответы на вопрос:

ilya494

Геометрия

4,6(94 оценок)

<АОС=150°

Объяснение:

обозначим вершины треугольника А В С, а его биссектрисы АЕ и СК, а точку их пересечения О. Большую сторону видно под углом АОС, поскольку большая сторона лежит напротив большего угла, поэтому большей стороной будет АС, поскольку она лежит напротив угла В=120° из ∆АВС и

угла АОС из ∆АОС. Мы можем найти угол АОС. Так как биссектриса делит угол пополам, то <ВАЕ=<ЕАС и <ВСК=<АСК. Так как сумма углов треугольника составляет 180°, то в ∆АВС: <А+<С=180–120=60°.

Рассмотрим полученный ∆АОС. Если <А+<С=60°, то <ОАС+<ОСА=60÷2=30°, поскольку эти углы разделены биссектрисами пополам и соответственно сумма этих углов будет в 2 раза меньше суммы углов А и С. Помним, что сумма углов треугольника составляет 180°, поэтому в ∆АОС <В=180–(<ОАС+<ОСА)=180–30=150°

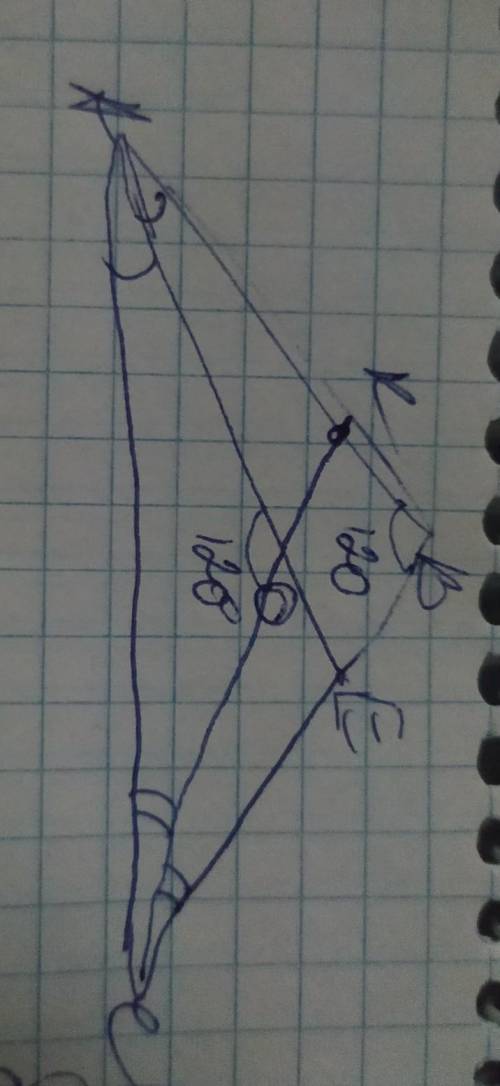
Більший кут трикутника дорівнює 120°. Під яким кутом видно більшу сторону цього трикутника з точки п

tanyaoganesova

Геометрия

4,4(91 оценок)

обозначим начало наклонной а, конец наклонной в ( точка пересечения с плоскостью α).

опустим из а перпендикуляр на плоскость α.

вс- проекция наклонной а.

ас⊥вс.

угол авс=45°

прямую b обозначим вк; угол авк=60°

рассмотрим треугольник авс.

так как угол авс=45°, то угол вас=45°,

треугольник авс прямоугольный равнобедренный.

ас=вс=а*sin(45°)=(a√2): 2.

треугольник авк прямоугольный.

вк=а*cos(60°)=а: 2

треугольник вкс - прямоугольный с гипотенузой вс

cos ∠ kbc=bк: вс=(а: 2): (a√2): 2=1: √2. умножив числитель и знаменатель на √2, получим

cos ∠ kbc=√2): 2. это косинус 45°

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.