Регистрация Спросить otvet5GPT
133719
07.01.2023 17:50
Алгебра
Есть ответ 👍

Пусть f(x) = l a - 4 | х² + 4х + а - 5. Найдите, при каких значениях параметра а уравнение f(x) = 0 имеет ровно различных 2 решения, причем каждое из этих решений не превосходит единицы.​

291
296
Посмотреть ответы 2

Ответы на вопрос:

anya071101
anya071101
4,8(75 оценок)

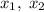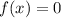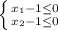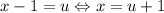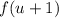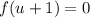Пусть x_{1},\; x_{2} — решения уравнения f(x)=0. По условию \left \{ {{x_{1}-1\leq 0 } \atop {x_{2}-1\leq 0 }} \right.. Можно сделать замену: x-1=u \Leftrightarrow x=u+1 и рассмотреть функцию f(u+1). Переформулируем условие: найти все значения параметра a, при каждом из которых уравнение f(u+1)=0 имеет два различных неположительных решения.

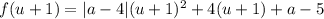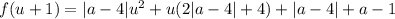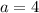f(u+1)=|a-4|(u+1)^2+4(u+1)+a-5, после преобразований получим f(u+1)=|a-4|u^2+u(2|a-4|+4)+|a-4|+a-1. Необходимым и достаточным условием неположительности решений явлется неположительность суммы и неотрицательность произведения корней. Применяя теорему Виета, переходим к системе: \left \{ {{-\frac{2|a-4|+4}{|a-4|}\leq 0 } \atop {\frac{|a-4|+a-1}{|a-4|}\geq 0 }} \right.. Сразу заметим, что a=4 не подходит, так как дает уравнение с не более чем одним решением. Система эквивалентна следующей: 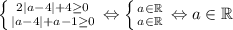\left \{ {{2|a-4|+4\geq 0 } \atop {|a-4|+a-1\geq 0 }} \right. \Leftrightarrow \left \{ {{a\in\mathbb{R}} \atop {a\in\mathbb{R}}} \right. \Leftrightarrow a\in\mathbb{R}(1)

Теперь нужно наличие двух различных решений. Здесь удобно вернутся к изначальному уравнению (так как мы просто двигали параболу горизонтально). 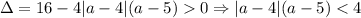\Delta=16-4|a-4|(a-5)0 \Rightarrow |a-4|(a-5), это неравенство эквивалентно системе: 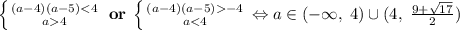\left \{ {{(a-4)(a-5)4} } \right.\;\textbf{or}\; \left \{ {{(a-4)(a-5)-4} \atop {a(2).

Пересекая (1) с (2) получим ответ.

ответ: 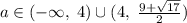a\in(-\infty,\; 4)\cup(4,\; \frac{9+\sqrt{17}}{2})

manilipitaozk746
manilipitaozk746
4,8(37 оценок)
1.  16x³+8x² +x=0  х(16x²+8x+1)=0   x₁=0     16x²+8x+1=0   d=64-4*16*1=0  x₂,₃ =-8/32 = -1/4 ответ: х∈(-1/4; 0) 2.    x³-2x² -36x+72=0  (x-2)(x²) +  (x-) =  (x-2)(x²-36)  =  (x - 2) (x + 6)(x - 6)  = 0    1) х-2=0        х₁=2   2) х+6=0      х₂=-6   3) х-6=0       х₃=6 ответ: х∈(-6; 2; 6)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS