08.04.2021 19:48

Есть ответ 👍

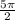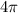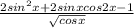
Решить уравнение 2) укажите корни этого уравнения, принадлежащие отрезку [ $\frac{5\pi }{2}$ и $4\pi$ ] $\frac{2sin^{2} x + 2sinx cos2x - 1 }{\sqrt{cosx} }$

161

272

Ответы на вопрос:

4,4(52 оценок)

Ниже↓

Объяснение:

Числитель 2sin²x+2sinx*cos2x-1=

=2sin²x+2sinx*(cos²x-sin²x)-(sin²x+cos²x)=

=sin²x- cos²x +2sinx*(cos²x-sin²x)=

=(sin²x- cos²x) -2sinx*(sin²x-cos²x)=

=(sin²x- cos²x)(1 -2sinx)=-( cos²x- sin²x)(1 -2sinx)=cos2x(1 -2sinx).

{cos2x(1 -2sinx)=0

{cosx≠0

Решим первое cos2x(1 -2sinx)=0

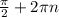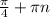1) cos2x=0, 2х= $\frac{\pi }{2} +2\pi n$ , х= $\frac{\pi }{4} +\pi n$ , n∈Z

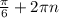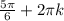2) 1 -2sinx=0 , sinx=1\2 , х= $\frac{\pi }{6} +2\pi n$ x= $\frac{5\pi }{6} +2\pi k$ , n,к∈Z

Решим второе

cosx≠0 , х≠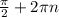 $\frac{\pi }{2} +2\pi n$ . Все найденные корни из п 1 подходят.

Выберем корни из [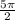 $\frac{5\pi }{2}$ ;4π ]

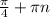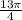Для х= $\frac{\pi }{4} +\pi n$ это $\frac{13\pi }{4}$ ,

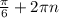Для х= $\frac{\pi }{6} +2\pi n$ это нет

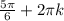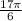Для х= $\frac{5\pi }{6} +2\pi k$ это $\frac{17\pi }{6}$ .

4,4(13 оценок)

2*x^3 + 12*x^2 + 18*x - (3*x)*(x - 1)*(x + 8) = x^2*(-x-9)+21 2*x^3 + 12*x^2 + 18*x - 21*x^2 - 3*x^3 + 24*x = x^2*(-x-9)+21 -21 + 42*x = 0 x = 1/2

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.