Ответы на вопрос:
ОДЗ:
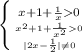
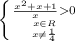 ⇒ x ∈( 0 ;
⇒ x ∈( 0 ; 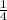 ) U (
) U ( 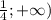
Если
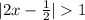 логарифмическая функция возрастает, большему значению функции соответствует большее значение аргумента:
логарифмическая функция возрастает, большему значению функции соответствует большее значение аргумента:
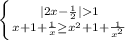
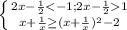 ⇒ замена переменной
⇒ замена переменной 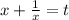
D=(-1)²-4·(-2)=9; корни t₁=1; t₂=2
C учетом ОДЗ:
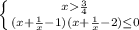 ⇒ x^2-2x+1 ≤0 ⇒ (x-1)²≤0 ⇒ x=1
⇒ x^2-2x+1 ≤0 ⇒ (x-1)²≤0 ⇒ x=1
Если
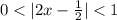 логарифмическая функция убывает, большему значению функции соответствует меньшее значение аргумента:
логарифмическая функция убывает, большему значению функции соответствует меньшее значение аргумента:
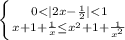
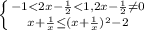 ⇒ замена переменной
⇒ замена переменной 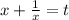
D=(-1)²-4·(-2)=9; корни t₁=1; t₂=2
C учетом ОДЗ:
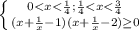 ⇒ x^2-2x+1 ≥0 ⇒(x-1)²≥0 x - любое
⇒ x^2-2x+1 ≥0 ⇒(x-1)²≥0 x - любое
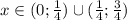
О т в е т. 
ОДЗ:
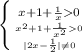
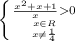 ⇒ x ∈( 0 ;
⇒ x ∈( 0 ; 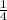 ) U (
) U ( 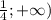
Применяем метод рационализации логарифмических неравенств:
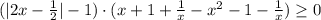
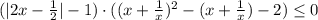
Решаем неравенство методом интервалов:
1)
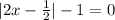 ⇒
⇒ 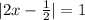 ⇒
⇒
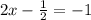 или
или 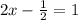
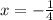 не входит в ОДЗ или
не входит в ОДЗ или 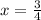
2)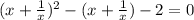
Замена 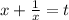
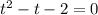
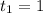 или
или 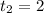
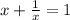 или
или 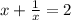
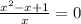 или
или 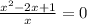
нет корней или x=1
Расставляем знаки неравенства
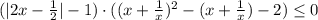
на ОДЗ:
(0) _-___ ( 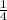 ) _____-____ (
) _____-____ ( 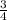 ) ____+_____ [1} ___+___
) ____+_____ [1} ___+___
О т в е т.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Выполните деление и запишите результат в один из трех столбцов в зависимости...
 zai4onok198819.12.2020 16:50
zai4onok198819.12.2020 16:50 -
Два мешка с капустой весят46 кг. один мешок на 6кг. тяжелее другого. сколько...
 Битсухатян04.11.2020 19:36
Битсухатян04.11.2020 19:36 -
6000: 3 столбиком потом 900: 2 столбиком потом 192: 4 столбиком решить...
 Sfdfgc30.08.2022 09:01
Sfdfgc30.08.2022 09:01 -
Назвать команду по .только не детские названия...
 алина388230.01.2021 12:00
алина388230.01.2021 12:00 -
Вид спорта, где проявляется гибкость а) хоккей б) баскетбол в) фигурное катание?...
 Сашаawalon20.01.2022 01:53
Сашаawalon20.01.2022 01:53 -
Какие и зданных величин можно вычесть из вместимости 250? выполни вычитание...
 хели310.02.2022 09:01
хели310.02.2022 09:01 -
Ров первого деревянного кремля имел глубину 5 м.,что на 2м. больше,чем его...
 8orzakt22.09.2020 00:27
8orzakt22.09.2020 00:27 -
Через 16 лет антон будет старше в три раза чем теперь. сколько ему лет сейчас?...
 katizh04.05.2020 03:37
katizh04.05.2020 03:37 -
Увеличте 80 рублей на 2\5 этой суммы...
 big3125.12.2020 07:37
big3125.12.2020 07:37 -
Найдите значение a , если: а) -а = 8.6...
 Hi166688888821.02.2020 06:44
Hi166688888821.02.2020 06:44

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
