Математика: До ть будь ласка з 3.1

путникспутник

12.01.2021 01:57

Математика

Есть ответ 👍

До ть будь ласка з 3.1

230

258

Посмотреть ответы 2

Ответы на вопрос:

odyvanchik22

Математика

4,6(26 оценок)

Пошаговое объяснение:

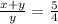
$\frac{x + y}{y} = \frac{5}{4}$

перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:

4(х+у)=5у

4х+4у=5у

4х=5у–4у

4х=у

х=у/4

Теперь подставим значение х в уравнение:

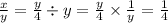
$\frac{x}{y} = \frac{y}{4} \div y = \frac{y}{4} \times \frac{1}{y} = \frac{1}{4}$

ОТВЕТ: х/у=1/4

2) Теперь это же значение у/4 подставим во второе уравнение:

(2√у+√х)/√х=(2√у+√у/√4)÷√у/√4=

=(2√у+√у/2)÷√у/2=((4√у+√у)/2)×2/√у=

=5√у/2×2/√у=5

ОТВЕТ: 5

ЗАДАНИЕ 2

во втором задании мы нашли чему будет =а: а=9b/4. Подставим его в первое уравнение:

1) a/b=9b/4÷b=9b/4×1/b=9/4=2,25

ОТВЕТ: 2,25

2) (а–b)/b=5/4 перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:

4(a–b)=5b

4a–4b=5b

4a=5b+4b

4a=9b

a=9b/4

теперь подставим значение а в уравнение:

(3√b+√a)/√a=(3√b+√9b/√4)/√9b/√4=

=(3√b+3√b/2)×√4/√9b

=((6√b+3√b)/2)×2/3√b=9√b/2×2/3√b=3

ОТВЕТ: 3

kvashenko403

Математика

4,5(71 оценок)

Вычислим предел интеграла где интеграл берётся по контуру, состоящему из верхней полуокружности и отрезка [-r, r], обходимому в положительном направлении. с одной стороны, этот интеграл можно представить в виде суммы интегралов по дуге и отрезку, притом в силу леммы жордана интеграл по дуге стремится к нулю, так как с другой стороны, этот интеграл можно взять при вычетов. под интегралом стоит мероморфная функция, имеющая простые полюсы в корнях 4-й степени из -1. в контур интегрирования два из них, и . значения вычета функции f(z) / g(z) в простом полюсе z=z0, если f(z) не имеет особенностей в точке z0, а g(z) дифференцируема, вычисляются по формуле f(z0) / g'(z0).

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.