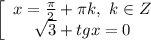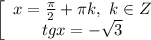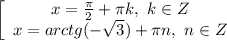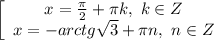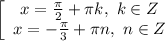Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
На фермерском рынке 8 торговце продали клубнику каждый назначил свою цену...
 abbasova0513.07.2021 10:10
abbasova0513.07.2021 10:10 -
Решите уравнение: (x+3)( x-1,3)=0...
 Nastya2861221.11.2021 21:35
Nastya2861221.11.2021 21:35 -
Азамат прочитал книгу за 3 дня.В первый день он прочитал 36%всей книги,во...
 MR3AlI01.10.2021 22:50
MR3AlI01.10.2021 22:50 -
Приведи 5 примеров смешанных чисел...
 Вика31038716.04.2021 18:26
Вика31038716.04.2021 18:26 -
7. Yeryong oqni tozalaganda 60 foizi po choqqa chiqib ketadi. Narxi 2000 so...
 Danilakazan57020.05.2022 11:26
Danilakazan57020.05.2022 11:26 -
5. Периметр прямоугольника 34 см, ширина 8 см. Найдите площадь. 1) 17 см2;...
 Kirillastrovskiy11.11.2020 03:28
Kirillastrovskiy11.11.2020 03:28 -
Нужно у выражение очень...
 polinaasya18.06.2022 20:40
polinaasya18.06.2022 20:40 -
решить задания на тему Відсотки. Відсоткові розрахунки ....
 АнтохаПрограммист28.05.2020 05:29
АнтохаПрограммист28.05.2020 05:29 -
ЛЮДИИИИИИИИ У выражение вычистлите его ачение: 0,3а*1,2 если а =0,05...
 Kurbakovli11.10.2020 02:25
Kurbakovli11.10.2020 02:25 -
Установите соответствие между пропорцией и ее решением : 16/х=2/3. 5/х=0,3/6.х/2=3,6/9...
 crazy66009.07.2021 01:19
crazy66009.07.2021 01:19

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.