З точки до площини трикутника зі сторонами 13,14 і 15 см проведено перпендикуляр основа якого вершина кута протилежного до сторони 14 см.ВІдстань від даної точки до цієї сторони дорінює 20 см.Знайдіть відстань від точки до площини трикутника

217

483

Посмотреть ответы 2

Ответы на вопрос:

elena232014

Геометрия

4,8(90 оценок)

ДВ=16см

обозначим вершины треугольника А В С, а точку от которой проведён перпендикуляр Д к вершине В: перпендикуляр ДВ. Наклонная, проведённая к стороне АС пересекает её в точке Н. Нам нужно найти перпендикуляр ДВ. Для этого проведём от вершины В высоту ВН к стороне АС=14см. Высота ВН является проекцией наклонной ДН. Найдём высоту через площадь ∆АВС по формуле Герона:

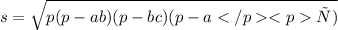
$s = \sqrt{p(p - ab)(p - bc)(p - aс)}$

где р- полупериметр, а ab, bc, ac - стороны ∆АВС.

Найдём периметр треугольника:

Р=13+14+15=42; Р/2=42÷2=21см

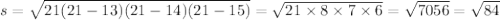
$s = \sqrt{21(21 - 13)(21 - 14)(21 - 15)} = \sqrt{21 \times 8 \times 7 \times 6} = \sqrt{7056} = \sqrt{84}$

Итак: S=84см².

Теперь найдём ВН, зная площадь и сторону треугольника, используя формулу площади:

S=1/2×АС×ВН

ВН=S÷1/2÷AC=84×2÷14=168÷14=12см

Наклонная ДН, её проекция на площадь треугольника ВН и перпендикуляр ДВ образуют прямоугольный треугольник с катетами

ВН и ДВ и гипотенузой ДН. Найдём искомый катет, он же перпендикуляр ДВ по теореме Пифагора:

ДВ²=ДН²– ВН²=20²-12²=400-144=256; ДВ=√256=16см

З точки до площини трикутника зі сторонами 13,14 і 15 см проведено перпендикуляр основа якого вершин

ProgramAkkaunt

Геометрия

4,5(55 оценок)

Из теоремы прямоугольного треугольника следует что если ав=ао=(х) то ов=(х)корень из 2 т е отрезок ав= тоже 4

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.