Cos в квадрате 2x + cos в квадрате 6x=1, принадлежащие отрезку [0; Пи/4]
132
137
Ответы на вопрос:
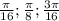
Объяснение:
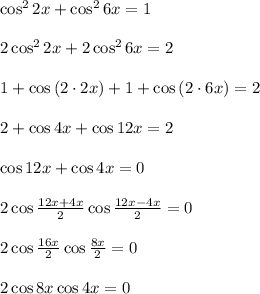
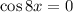 или
или 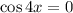
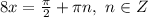 или
или 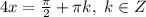
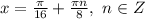 или
или 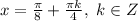
Отберем корни уравнения, принадлежащие отрезку ![[0;\frac{\pi}{4} ]](/tpl/images/3780/9368/59225.png) :
:
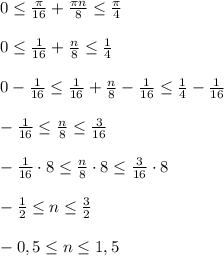
так как n-целое число, то 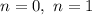
если 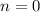 , то
, то 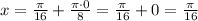
если 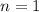 , то
, то 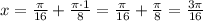
2.
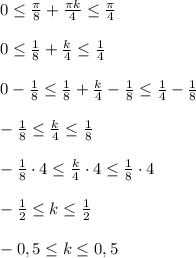
так как n-целое число, то 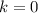
если 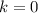 , то
, то 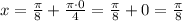
=========================
![\frac{\pi}{16}; \frac{\pi}{8}; \frac{3\pi}{16}\in [0;\frac{\pi}{4} ]](/tpl/images/3780/9368/cc5e7.png)
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Геометрия
-
Прямоугольный треугольник ABC вращается вокруг гипотенузы, длина которой 40...
 Анетта66627.01.2021 07:34
Анетта66627.01.2021 07:34 -
Решить карточку по теме геометрические тела с чертежом...
 dhhdhhd5515.02.2023 11:00
dhhdhhd5515.02.2023 11:00 -
дано паралелепіпед сторони основи 10 см і 17 см одна з діагоналей основи 21см...
 ankreinas04.02.2023 13:25
ankreinas04.02.2023 13:25 -
Основа прямої призми – прямокутний трикутник з гіпотенузою а(альфа) і гострим...
 eromadima21.04.2020 09:45
eromadima21.04.2020 09:45 -
Дано три точки на плоскости. A (1,-2) B (3,-6) C (1,2). Найти расстояние от...
 uldairuslanova01.09.2022 02:48
uldairuslanova01.09.2022 02:48 -
в основі піраміди лежить прямокутний трикутник зі сторонами 4см, 5см і 7см,...
 27Alisa37112.06.2022 11:53
27Alisa37112.06.2022 11:53 -
Знайти кут NOM якщо кут NMN =53° РЕШИТЬ...
 ПУШОК23408.12.2020 13:26
ПУШОК23408.12.2020 13:26 -
Даны векторы {2; –4; 3} и {–3; 1; 1}.Найдите координаты вектора = 0,3 -2 ....
 MrCapuchino15.03.2023 11:08
MrCapuchino15.03.2023 11:08 -
Между пунктами A и B находится болото. Чтобы найти расстояние между A и B, отметили...
 аза10115.09.2021 05:43
аза10115.09.2021 05:43 -
Радиус сферы равен 4. Площадь большого круга сферы равна...
 lalka13723.06.2021 03:18
lalka13723.06.2021 03:18

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
