perrrii

05.04.2021 08:06

Есть ответ 👍

Как подступиться к решению такого уравнения?Если можно, то с примером решения этого или подобного уравнения

169

255

Посмотреть ответы 3

Ответы на вопрос:

АленаКонева

Математика

4,6(72 оценок)

√3сosx-√2cos²x+√2sin²x+√3sinx=0

√3sinx+√3сosx-√2(cosx-sinx)(cosx+sinx)=0

(cosx+sinx)(√3-√2cosx+√2sinx)=0

cosx+sinx=0;tgx=-1; х=-π/4+πn; n∈Z;

(sinx-cosx)=-√(3/2)

(sinx-sin(π/2-x)=-√(3/2)

2sin(x-π/4)*cosπ/4=-√(3/2);

√2sin(x-π/4)=-√(3/2);

sin(x-π/4)=-√(3/4);

(x-π/4)=(-1)ⁿ⁺¹arcsin√0.75+πк; к∈Z

x=π/4+(-1)ⁿ⁺¹arcsin√0.75+πк; к∈Z

skata9196

Математика

4,4(46 оценок)

1. Обратить внимание на аргументы. Здесь есть и х, и 2х.

Значит надо все аргументы свести к одному аргументу х,

применив формулу косинуса двойного аргумента

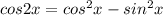
cos2x=cos^2x-sin^2x

Уравнение :

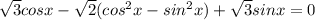
$\sqrt{3} cosx-\sqrt{2} (cos^2x-sin^2x)+\sqrt{3} sinx=0$

Разложим на множители:

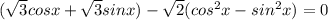
$(\sqrt{3} cosx+\sqrt{3} sinx)-\sqrt{2}( cos^2x-sin^2x)=0$

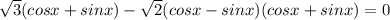
$\sqrt{3} (cosx+sinx)-\sqrt{2}( cosx-sinx)(cosx+sinx)=0$

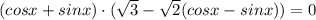
$(cosx+sinx)\cdot (\sqrt{3}-\sqrt{2}( cosx-sinx))=0$

Произведение двух множителей равно 0 когда хотя бы один из них равен 0:

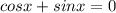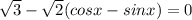
cosx+sinx=0 или $\sqrt{3}-\sqrt{2}( cosx-sinx)=0$

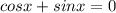cosx+sinx=0 - однородное тригонометрическое уравнение первого порядка, делим на cosx ≠0

tgx=-1

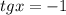
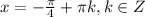
$x=-\frac{\pi }{4} +\pi k, k\in Z$

или

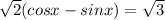
$\sqrt{2}( cosx-sinx)=\sqrt{3}$

Так как

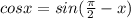
$cosx=sin(\frac{\pi }{2} -x)$

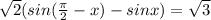
$\sqrt{2}( sin(\frac{\pi }{2} -x)-sinx)=\sqrt{3}$

Применяем формулу

sinα - sinβ=

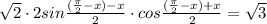
$\sqrt{2}\cdot 2 sin \frac{(\frac{\pi }{2} -x)-x}{2}\cdot cos\frac{(\frac{\pi }{2} -x)+x}{2}=\sqrt{3}$

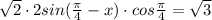
$\sqrt{2}\cdot 2 sin (\frac{\pi }{4} -x)\cdot cos\frac{\pi }{4}=\sqrt{3}$

так как $cos\frac{\pi }{4}=\frac{\sqrt{2}}{2}$

$\sqrt{2}\cdot 2 sin (\frac{\pi }{4} -x)\cdot \frac{\sqrt{2}}{2}=\sqrt{3}$

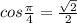
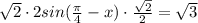
$sin (\frac{\pi }{4} -x)=\frac{\sqrt{3}}{2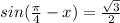}$ так как синус - нечетная функция, то

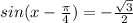
$sin (x-\frac{\pi }{4} )=-\frac{\sqrt{3}}{2}$

Общий вид решения уравнения:

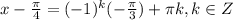
$x-\frac{\pi }{4} =(-1)^{k}(-\frac{\pi}{3})+ \pi k, k \in Z$

Это удобнее записать в виде серии двух ответов:

k=2m или k = 2n-1

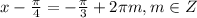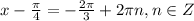
$x-\frac{\pi }{4} =-\frac{\pi}{3}+2 \pi m, m \in Z$ или $x-\frac{\pi }{4} =-\frac{2\pi}{3}+2 \pi n, n \in Z$

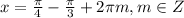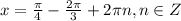
$x=\frac{\pi }{4} -\frac{\pi}{3}+2 \pi m, m \in Z$ или $x=\frac{\pi }{4} -\frac{2\pi}{3}+2 \pi n, n \in Z$

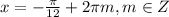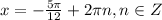
$x= -\frac{\pi}{12}+2 \pi m, m \in Z$ или $x= -\frac{5\pi}{12}+2 \pi n, n \in Z$

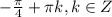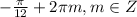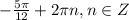
О т в е т. $-\frac{\pi }{4} +\pi k, k\in Z$ ; $-\frac{\pi}{12}+2 \pi m, m \in Z$ ; $-\frac{5\pi}{12}+2 \pi n, n \in Z$

ира8800

Математика

4,5(90 оценок)

что? я не поняла, что?*$*#*#

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.