Регистрация Спросить otvet5GPT
Andrey200694
17.06.2021 11:33
Математика
Есть ответ 👍

1) Докажите, что равенство 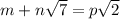m+n\sqrt7=p\sqrt2 не выполнено ни для каких целых m, n, и p, не равных одновременно нулю. 2) Найдите какие-нибудь такие целые m, n, и p, не равные одновременно нулю, что 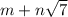m+n\sqrt7 отличается от 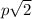p\sqrt2 не более, чем на 0,01. Если таких m, n и p не существует, объясните, почему.

133
278
Посмотреть ответы 2

Ответы на вопрос:

XWaeRr
XWaeRr
4,8(37 оценок)

1) Пусть равенство 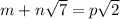m+n\sqrt{7}=p\sqrt{2} выполнено. Тогда выполнено и равенство 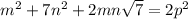m^2+7n^2+2mn\sqrt{7}=2p^2, но слева иррациональное число, а справа целое, противоречие.

2) Пусть сразу 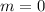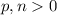m=0, p,n0. Тогда нам нужно найти как можно меньшее значение 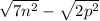\sqrt{7n^2}-\sqrt{2p^2}. Мы сможем этого достичь, если числа 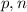p,n будут достаточно большими, а величина 7n^2-2p^2 достаточно маленькой.

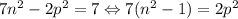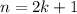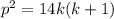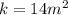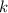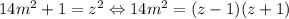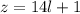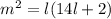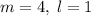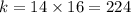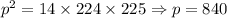Найдем такие числа. Пусть 7n^2-2p^2=7 \Leftrightarrow 7(n^2-1)=2p^2, возьмем n=2k+1. Получим p^2=14k(k+1), пусть k=14m^2, тогда требуется найти такое k, чтобы 14m^2+1=z^2 \Leftrightarrow 14m^2=(z-1)(z+1), сделаем последнюю замену: z=14l+1, имеем: m^2=l(14l+2), откуда сразу угадывается решение m=4,\;l=1. 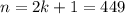Возвращаясь к заменам, получим k=14\times16=224, Значит, p^2=14\times224\times 225\Rightarrow p=840, n=2k+1=449.

Теперь осталось проверить: 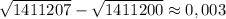\sqrt{1411207}-\sqrt{1411200}\approx 0,003. Итак, решением будет тройка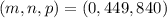 (m,n,p)=(0,449,840)

Алекс2521
Алекс2521
4,4(98 оценок)

х=яблок у 1 мальчика у=яблок у 2 мальчика х +у=15,2*(х-4)=у+4 2х-8=у+4 у=2х-12 2х-12+х=15 3х=27 х=9 столько яблок у 1 го х=6 у 2 го

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS