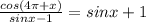Регистрация Спросить otvet5GPT
twenty21
01.10.2021 09:16
Алгебра
Есть ответ 👍

Найдите корни уравнения, принадлежащие отрезку [-3pi/2;0] \frac{cos(4\pi+x) }{sinx-1} = sinx+1

243
383
Посмотреть ответы 3

Ответы на вопрос:

ммммм89
ммммм89
4,6(84 оценок)

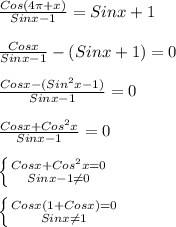
\frac{Cos(4\pi+x) }{Sinx-1}=Sinx+1\\\\\frac{Cosx}{Sinx-1} -(Sinx+1)=0\\\\\frac{Cosx-(Sin^{2}x-1)}{Sinx-1}=0\\\\\frac{Cosx+Cos^{2}x }{Sinx-1} =0\\\\\left \{ {{Cosx+Cos^{2}x=0 } \atop {Sinx-1\neq0 }} \right. \\\\\left \{ {{Cosx(1+Cosx)=0} \atop {Sinx\neq1 }} \right.

или  Cosx = 0    или Cosx = - 1

Cosx = 0 - не подходит, так как если Cosx = 0 , то Sinx = 1 , а это недопустимо .

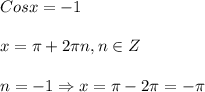
Cosx = - 1\\\\x= \pi +2\pi n,n\in Z\\\\n=-1\Rightarrow x=\pi -2\pi=-\pi

Nastya162005
Nastya162005
4,7(31 оценок)

ОДЗ : sinx≠1 ;x≠π/2+2πn; n∈Z ;

cos(4π+x)=cosx;

приведем к общему знаменателю.

cosx=-(1-sin²x)=0; cosx+cos²x=0; cosx*(1+cosx)=0;  

1)cosx=0⇒x=π/2+πk; k∈Z

учитывая ОДЗ, надо взять только нечетные к, т.е. х=3π/2+ 2πk; k∈Z; т.к. при четных к обращается в нуль знаменатель.

2) cosx=-1;  x=π+2πm; m∈Z;

Найдем корни, принадлежащие [-3π/2;0]

1) х=3π/2+ 2πk; k∈Z; к=-1; х=3π/2-2π=-π/2∈[-3π/2;0] ;к=-2; х=3π/2-4π=

-5π/2∉[-3π/2;0]

2) x=π+2πm; m∈Z; m=-1; x=π-2π=-π∈[-3π/2;0], остальные можно не проверять, т.к. они выходят за пределы рассматриваемого отрезка.

qooperty
qooperty
4,8(39 оценок)
Ах+ау+аz = a(x+y+z) xy  -xz- 5x  = x(y - z  - 5) 

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS