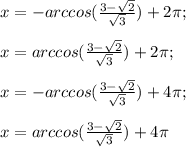Sin(π3−x)+cos(π6−x)=3–√ 2. Найдите корни этого уравнения, принадлежащие отрезку [π/2;9π/2].
224
446
Ответы на вопрос:
S= 36 см²
Пошаговое объяснение:
Делим фигуру на два прямоугольника и находим их площадь по формуле S=a×b
S¹= 11×2= 22см²
S²= 7×2=14 см²
Находим площадь всей фигуры:
S= 22+14= 36 см²
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
517440:924 В сТОЛБИК...
 dias110121.04.2022 12:32
dias110121.04.2022 12:32 -
Есептеңдер 507 5 класс 1часть пом ...
 момалог02.09.2020 11:41
момалог02.09.2020 11:41 -
370. Реши уравнения. х: 9 = 1 000 – 9 10 х: 9 = 1 000 – 9 10 100 х=2 430 – 2030...
 ДашаУмняшаТ22.03.2021 16:23
ДашаУмняшаТ22.03.2021 16:23 -
Какова область значений функции y=2x ?...
 Кэти30513.09.2020 20:15
Кэти30513.09.2020 20:15 -
1539645*7926478+66286489-6388478...
 kapcha22807.06.2023 09:04
kapcha22807.06.2023 09:04 -
Какое из оснований, формулы которых даны, является щёлочью? Cr(OH)3 Pd(OH)2 Ca(OH)2...
 tyty5516.10.2021 07:59
tyty5516.10.2021 07:59 -
Найдите значения коэффициентов -20*4a+90a+10y...
 kshig02.02.2021 17:03
kshig02.02.2021 17:03 -
Вычисли,используя распредельное свойство. 3,12 * 7,1 - (-0,8) * 6,12...
 Кактус131324.10.2020 07:17
Кактус131324.10.2020 07:17 -
Составь задачу по таблице и реши её спальная комната длина ширина площадь 5м одинак...
 exomashka01.09.2021 23:19
exomashka01.09.2021 23:19 -
(+2)•[(+5)-(3)]= ответ...
 М4ш407.08.2021 07:10
М4ш407.08.2021 07:10

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

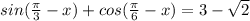
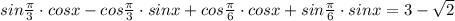
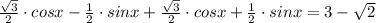
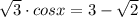
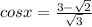 ⇒
⇒ 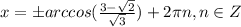
![[\frac{\pi }{2};\frac{9\pi }{2} ]](/tpl/images/3780/7439/96f5f.png) принадлежат 4 корня:
принадлежат 4 корня: