Ответы на вопрос:
ответ: 128 , при x=y=z=2
Объяснение:
u=z*x^2*y^3*(14-2x-3y-z) , где x,y,z>0
Очевидно, раз нам нужно наибольшее значение, то нам есть смысл рассматривать только те значения, при которых 14-2x-3y-z>=0
0<2x+3y+z<=14
В рассматриваемой области из неравенства Коши-Буняковского имеем :
z*x^2*y^3 = z*x*x*y*y*y<= ( (2x+3y+z)/6)^6
Откуда:
u<=6^(-6) * ( (2x+3y+z))^6 *(14-(2x+3y+z) )
Пусть : 2x+3y+z=t
0<t<=14
Найдем максимум функции:
f(t) = t^6 *(14-t) =14t^6 -t^7
Найдем нули производной:
f'(t) = 84t^5-7*t^6 = 0
t1=0
84-7t=0
t2=84/7 = 12 - точка максимума.
f(14)=f(0)=0
f(12) = 2*12^6 - максимальное значение на 0<t<=14
Таким образом:
u<=6^(-6) * ( (2x+3y+z))^6 *(14-(2x+3y+z) ) <= 6^(-6) *2*12^6 = 2^7 = 128. Иначе говоря, umax = 128
Данное значение будет получено, когда:
x=y=z ( требование выполнения равенства в неравенстве Коши-Буняковского), и когда 2x+3y+z = 12 или 6x=12 → x=y=z=2
Объяснение:
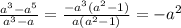
1) Вынести из числителя общий множитель -а³
2) Вынести из знаменателя общий множитель а
3) сократить а²-1
4) поделить -а³ на а = -а^(3-1)=-а²
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Вычисли x, если y равно 26, используя данную формулу: y=3x+2 ответ:...
 Антонggez27.01.2022 15:59
Антонggez27.01.2022 15:59 -
Содного участка собрали 450 т, а с другого, площадь которого на...
 AkiraK66601.12.2022 04:37
AkiraK66601.12.2022 04:37 -
Решить неравенство: (3х+4)√(4-х²)≥0...
 MoLoDaYa66601.03.2023 15:08
MoLoDaYa66601.03.2023 15:08 -
Укажите все формулы сокращенного умножения и прикрепите к ним 5...
 vasiljev25507.03.2021 03:16
vasiljev25507.03.2021 03:16 -
20 ! 1. разность двух чисел равна 25 найдите сумму этих чисел если...
 Svetic198518.04.2020 01:24
Svetic198518.04.2020 01:24 -
Назовем год таинственным если из его цифр можно составить некоторые...
 BatsonPlay29.05.2022 14:13
BatsonPlay29.05.2022 14:13 -
Разность суммы квадратов двух последовательных натуральных чисел...
 0106196921.04.2020 03:39
0106196921.04.2020 03:39 -
Решить систему уравнений: log4x-log2y=0, (4 и 2 это основания)...
 violagugu13.01.2021 04:26
violagugu13.01.2021 04:26 -
Выразить в градусной мере величины углов 5,3...
 hellday08.09.2021 18:31
hellday08.09.2021 18:31 -
Докажите,что не зависит от a значение выражения. (7,5а-2b)(2а+4b)-15a(a+2b)+4ab...
 Karinakotik20016501.09.2022 12:21
Karinakotik20016501.09.2022 12:21

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

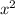
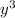 z(14-2x-3y-z) В области x,y,z >0
z(14-2x-3y-z) В области x,y,z >0