2004080111

24.11.2021 13:49

Геометрия

Есть ответ 👍

РАЗОБРАТЬСЯ

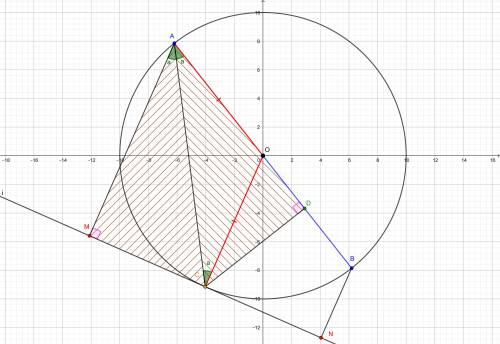
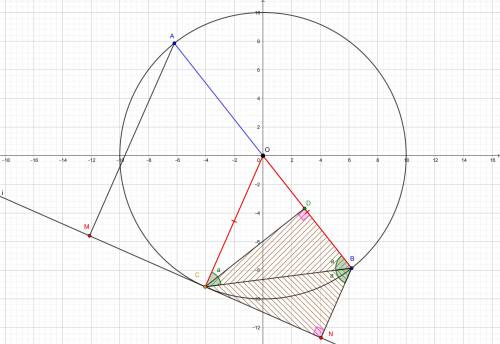
Прямая l касается окружности с диаметром AB в точке C; M и N — проекции точек A и B на прямую l, D — проекция точки C на AB. Докажите, что CD2 = AM . BN.

101

299

Посмотреть ответы 2

Ответы на вопрос:

sonyashestakova

Геометрия

4,6(55 оценок)

Доказательство:

1) См. рисунок 1

∠AMC = 90° т.к M - проекция A на l

∠)OCN = 90° т.к l - касательная к окружности в точке C, OC - радиус в точку касания

Следовательно AM || OC

Значит ∠MAC = ∠ACO

AO = OC (как радиусы) ⇒ ΔACO - равнобедренный ⇒ ∠CAO = ∠ACO

Значит ∠MAC = ∠CAO

∠MCA = 90 - a

∠DCA = 90 - a (∠CDA = 90° т.к D - проекция C на AB)

Следовательно ∠MCA = ∠DCA

Откуда следует, что ΔMAC = ΔDAC по стороне и двум углам (AC - общая)

А значит AM = AD

2) Аналогично доказывается BD = BN (см. Рисунок 2)

3) См. Рисунок 3.

∠ACB = 90° т.к опирается на диаметр

В ΔABC: ∠CAB = 90° - ∠CBD

В ΔCBD: ∠DCB = 90° - ∠CBD

Следовательно ∠CAB = ∠DCB

Откуда следует, что ΔABC подобен ΔCBD по двум углам.

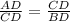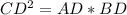
Значит $\frac{AD}{CD} = \frac{CD}{BD}$ ⇒ $CD^{2} = AD * BD$

Из пунктов 1 и 2:

AM = AD

BD = BN

Следовательно

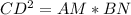
$CD^{2} = AM * BN$

Доказано

============

Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"

Бодрого настроения и добра!

Успехов в учебе!

РАЗОБРАТЬСЯ Прямая l касается окружности с диаметром AB в точке C; M и N — проекции точек A и B на п

карыч19

Геометрия

4,8(2 оценок)

Длина вектора определяется по формуле: |ab| =корень((х1-х2)^2+(у1-у2)^2)= =корень(())^2+())^2= =корень(5^2+12^2)= корень169=13 ответ 13

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.