Количество двузначных чисел, сумма цифр которых не менее произведения этих цифр, равно? (расписать решение и объяснить)

198

317

Посмотреть ответы 2

Ответы на вопрос:

shamilsaidov2

Математика

4,8(29 оценок)

27 чисел

Пошаговое объяснение:

Пусть x, y — цифры двузначного числа (1 ≤ x ≤ 9, 0 ≤ y ≤ 9). Тогда

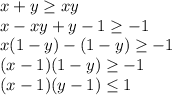
$x+y\geq xy\\x-xy+y-1\geq -1\\x(1-y)-(1-y)\geq -1\\(x-1)(1-y)\geq -1\\(x-1)(y-1)\leq 1$

Первый множитель не меньше нуля, а второй не меньше -1.

Если y = 0, то произведение заведомо отрицательно, и все x подходят (+9 вариантов);

Если y = 1, то произведение равно нулю, все x подходят (+9 вариантов);

Если y = 2, то 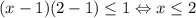$(x-1)(2-1)\leq 1\Leftrightarrow x\leq 2$ (+2 варианта);

Если y ≥ 3, то 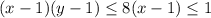$(x-1)(y-1)\leq 8(x-1)\leq 1$ . При x ≥ 2 произведение больше единицы, поэтому для каждого y подходит ровно один x = 1 (+7 вариантов).

Итого 27 чисел.

catmartovski

Математика

4,6(5 оценок)

4

Это точно лайк

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.