Треугольник ABC, AK - высота, H - ортоцентр. Окружность, проходящая через точки A и K, пересекает AB и AC в точках M и N соответственно. Через точку A проходит прямая, параллельная BC. Окружности AHM и AHN пересекают эту прямую в точках X и Y соответственно. Докажите, что XY=BC.

225

377

Посмотреть ответы 2

Ответы на вопрос:

Lulu117

Геометрия

4,7(27 оценок)

Пусть точка, в которой BC пересекает синюю окружность второй раз это K1. На приложенном к условию чертеже она немного левее точки K. Эта окружность проходит через точки A и K, а точка K1 может быть в произвольном месте, но её положение полностью определяет саму окружность.

Поскольку ∠K1KA = 90°; => K1A - диаметр синей окружности.

По этой же причине

∠K1NC = 90°; ∠K1MB = 90°

Поэтому K1M и K1N - перпендикулярны AB и AC, соответственно.

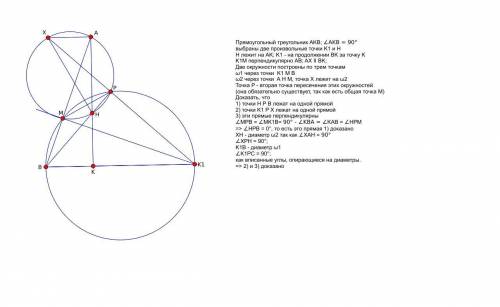
Прежде, чем решать саму задачу, см. рисунки 1 и 2, приложенные к решению. На них решается вс задача, нечто вроде леммы. Я сохранил обозначения, но важно! - что точка H там НЕ является ортоцентром - это произвольная точка на AK. Эта "лемма" доказана там для двух вариантов местоположения точки K1, когда точка H находится внутри отрезка AK. Интересующиеся могут попробовать исследовать другие варианты.

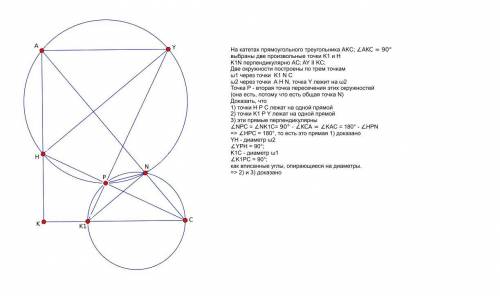
На третьем прилагаемом рисунке - чертеж для решения самой задачи.

Первый шаг - строится окружность по трем точкам A H M и еще одна - на BK1, как на диаметре, эта окружность пройдет через точку M, так как ∠K1MB = 90°. Точка P - это вторая точка пересечения этих окружностей (она есть обязательно, так как уже есть одна - точка M). Второй шаг - по доказанной лемме K1X проходит через точку P и перпендикулярно BH, которая тоже проходит через точку P.

И третье - теперь (вот только теперь!) надо вспомнить, что H - точка пересечения высот (ортоцентр) треугольника ABC, то есть XK1 II AC - обе прямые перпендикулярны BH; => K1XAC - параллелограмм, => XA = K1C;

Доказательство того, что BK1 = AY, аналогичное. => XY = BC; чтд.

Но есть еще более интересная штука. Треугольник K1XY вообще оказывается ЦС-отражением треугольника ABC относительно середины AK1 - центра синей окружности. Интересно, а нет ли тут какой-то гомотетии?

Треугольник ABC, AK - высота, H - ортоцентр. Окружность, проходящая через точки A и K, пересекает AB

LeMuRkA228

Геометрия

4,5(68 оценок)

180-36= 144. т.к они смежные. а сумма смежных углов 180 градусов

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.