Регистрация Спросить otvet5GPT
AndyXD
03.11.2020 12:41
Математика
Есть ответ 👍

в треугольнике АВС проведена высота ВD медиана ВМ и биссектриса ВК.докажите что точка К принадлежит отрезку DM.

230
431
Посмотреть ответы 3

Ответы на вопрос:

voznas
voznas
4,7(72 оценок)

Небольшая поправка. Если треугольник равнобедренный с основанием АС, то в нем все три основания высоты, биссектрисы и медианы сливаются в одну точку.

В Δ ABC точки  D, К и M - основания соответственно высоты, биссектрисы и медианы, проведенных из вершины B. Опишем около

Δ ABC окружность. Пусть Е - точка пересечения прямой BК с этой окружностью. Тогда Е будет серединой дуги AC. Поэтому прямая, проведенная через точку Е параллельно BD, перпендикулярна хорде AC и проходит через ее середину, т. е. точку M. А т.к. точки B и Е лежат по разные стороны от прямой AC, то точка К лежит между проекциями концов отрезка ЕB, т. е. между точками D и M, значит , она принадлежит отрезку DM, ч.т.д.

Polina230407
Polina230407
4,8(22 оценок)

ответ: Постарался доказать как можно более строго.

Пошаговое объяснение:

Рассмотрим неравнобедренный Δ ABC

Опишем около Δ ABC окружность .

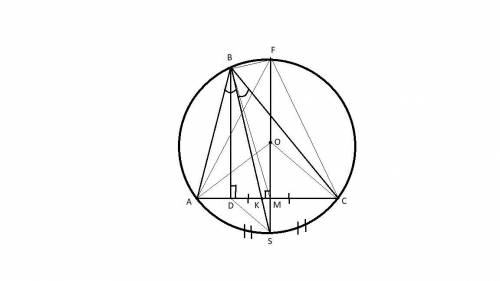
Проведем  к стороне AC отрезок OM и продлим его до диаметра окружности FS.

Δ AOC - равнобедренный, поскольку OA = OС  как радиусы окружности.  Таким образом, его медиана OM (M делит AC пополам) является и его высотой, но тогда и медиана FM  треугольника AFC является его высотой, а значит он так же равнобедренный. Но тогда, эта высота является и биссектрисой, то есть ∠AFS =∠SFC, причем эти углы вписаны в окружность, а значит опираются на равные дуги.  Иначе говоря, дуга AS равна дуге SC, но тогда и вписанные углы ∠ABS = ∠SBC .  

Таким образом, BS биссектриса ∠B треугольника ABC ,  пусть она пересекает сторону AC в точке K.

BD ║ FS как два перпендикуляра к одной прямой AC, то есть SDBF - трапеция, а  ЛЮБАЯ трапеция является выпуклым четырехугольником, причем BS ее диагональ. Теперь придется сослаться на одну аксиому, а именно, что все точки диагонали выпуклого четырехугольника лежат внутри четырехугольника, но тогда и точка K лежит внутри трапеции (K∈SDBF).

Геометрическое место точек, принадлежащих и трапеции и отрезку AC - это отрезок DM.

Таким образом, раз точка K∈AC и K∈ SDBF , то K∈DM

Что и требовалось доказать.


в треугольнике АВС проведена высота ВD медиана ВМ и биссектриса ВК.докажите что точка К принадлежит
ulyanooo
ulyanooo
4,5(66 оценок)
(5*5-5)5=100 5*5=24-5=20*5=100

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS