Регистрация Спросить otvet5GPT
comeback92
11.03.2023 09:02
Алгебра
Есть ответ 👍

Т36) Найдите наименьшее положительное решение уравнения cos^2(2x)= (2+ корень3)/4 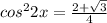{cos}^{2} 2x = \frac{2 + \sqrt{3} }{4}
Варианты ответа:

π/3 ; 2π/3 ; π/12 ; π/24

Заранее
​

168
338
Посмотреть ответы 2

Ответы на вопрос:

КатюшаШамец
КатюшаШамец
4,7(2 оценок)
Решение:

Уравнение:

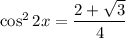
\cos^2 2x = \dfrac{2+\sqrt{3}}{4}

Предлагаю применить формулу косинуса половинного угла (она выглядит вот так: 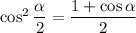\cos^2 \dfrac{ \alpha }{2} = \dfrac{1 + \cos \alpha }{2}):

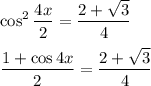
\displaystyle \cos^2 \frac{4x}{2} = \dfrac{2+\sqrt{3}}{4} \\\\\frac{1 + \cos 4x}{2} = \dfrac{2+\sqrt{3}}{4} \\

Теперь домножим обе части уравнения на четыре (чтобы "избавиться от дробей") + упростим получившееся выражение:

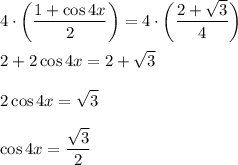
\displaystyle 4 \cdot \bigg ( \frac{1 + \cos 4x}{2} \bigg ) = 4 \cdot \bigg ( \dfrac{2+\sqrt{3}}{4} \bigg ) \\\\2 + 2 \cos 4x = 2 + \sqrt {3} \\\\2 \cos 4x = \sqrt{3} \\\\\cos 4x = \frac{\sqrt{3}}{2}

Мы получили выражение вида 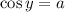\cos y = a (в нашем случае 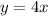y=4x). Оно решается по формуле: 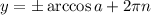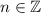y = \pm \arccos a + 2 \pi n, n \in \mathbb Z. Значит:

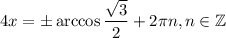
4x = \pm \arccos \dfrac{ \sqrt {3} }{2} + 2 \pi n, n \in \mathbb Z

А также вспомним, что 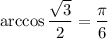\arccos \dfrac{ \sqrt {3} }{2} = \dfrac{\pi}{6}:

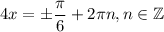
{ 4x = \pm \dfrac{ \pi }{6} + 2 {\pi n}, n \in \mathbb Z }

И, на всякие случай, поделим все на 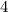4:

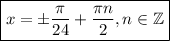
\boxed { x = \pm \dfrac{ \pi }{24} + \dfrac{\pi n}{2}, n \in \mathbb Z }

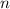Теперь найдем наименьшее положительное решение уравнения. Понятно, что \pi/24 нужно взять с "плюсом" (чтобы и в итоге получился "плюс"), а также n приравнять нолю:

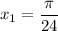
x_1 = \dfrac{\pi}{24}

Получился как раз последний вариант ответа!

ответ: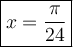

\large {\boxed {x = \dfrac{\pi}{24}}}

fifi17
fifi17
4,8(62 оценок)

тут выражен х и у, это верно, но запись не очень правильная

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS