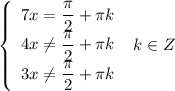Математика: Т40) Решите уравнение: tg(4x+π)*tg(3x) = 1 Заранее

shkuratov89525510021

29.06.2021 20:41

Математика

Есть ответ 👍

Т40) Решите уравнение: tg(4x+π)*tg(3x) = 1

Заранее

273

299

Посмотреть ответы 2

Ответы на вопрос:

maxim090

Математика

4,7(11 оценок)

$\text{tg}(4x + \pi) \cdot \text{tg} (3x) = 1$

$\text{tg}(4x) \cdot \text{tg} (3x) = 1$

$\dfrac{\sin (4x)}{\cos (4x)} \cdot \dfrac{\sin (3x)}{\cos (3x)} = 1$

$\dfrac{\sin (4x) \sin (3x)}{\cos (4x) \cos (3x)} - 1 = 0$

$\dfrac{\sin (4x) \sin (3x) - \cos (4x) \cos (3x)}{\cos (4x) \cos (3x)} = 0$

$\dfrac{\cos (4x) \cos (3x) - \sin (4x) \sin (3x)}{\cos (4x) \cos (3x)} = 0$

$\dfrac{\cos (7x)}{\cos (4x) \cos (3x)} = 0$

$\left\{\begin{array}{ccc}\cos (7x) = 0\\\cos (4x) \neq 0\\\cos (3x) \neq 0\end{array}\right$

$\left\{\begin{array}{ccc}7x = \dfrac{\pi}{2} + \pi k\\4x \neq \dfrac{\pi}{2} + \pi k\\3x \neq \dfrac{\pi}{2} + \pi k\end{array}\right \ k \in Z$

$\left\{\begin{array}{ccc}x = \dfrac{\pi}{14} + \dfrac{\pi k}{7} \\x \neq \dfrac{\pi}{8} + \dfrac{\pi k}{4} \ \\x \neq \dfrac{\pi}{6} + \dfrac{\pi k}{3} \ \end{array}\right \ k \in Z$

$x = \dfrac{\pi}{14} + \dfrac{\pi k}{7}, \ k \in Z$

ответ: $\text{B}) \ x = \dfrac{\pi}{14} + \dfrac{\pi k}{7}, \ k \in Z$

Irina5786

Математика

4,4(69 оценок)

1470: 2=735 588 : 2=294 735: 3=245 294: 2=147 245: 5=49 147: 3=49 49: 7=7 49: 7=7 7: 7=1 7: 7=1 1 1 (нок)=2

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Sasha1234679
02.01.2021 00:47

48 тонна 9 килограмм =?кг...
МАВ03022004
09.10.2020 17:16

Содержание шерсти в шапке, варежках и жилетке 680 г. В шапке в 4 раз...
Milenochka2006
16.05.2022 22:41

1) 4|x-13|=16; 2) 5|x+21|+6=26...
sofmeo
02.06.2021 23:26

-48,17/35+(11,4/35-18,61/70)...
drmkhva
11.03.2022 09:28

На 240 р. дороже. Сколько стоит каждый кусок? (карточка 154) Работа...
Ertadaysma
10.06.2021 10:52

Найти сумму чисел 18 и -9...
ксю882
02.02.2020 22:30

Що значит : Выводити на чисту воду...
aslanovrusik44
18.01.2021 22:55

Решите уравнение: 3x=360000...
Незнайкаа11
26.06.2021 18:18

Математика 446 номер 6 класс...
tigranpesoz3twi
19.11.2021 18:43

Найдите объем тела а) б) в) г)...

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.