Математика: Решите егэ по профилю

islamovaemilia1

30.12.2021 05:05

Математика

Есть ответ 👍

Решите егэ по профилю

265

339

Посмотреть ответы 2

Ответы на вопрос:

azaliyazaynulinnf

Математика

4,7(67 оценок)

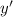Чтобы найти критическую точку, нужно найти такие , при которых функция (производная 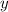) равна 0.

Будем пользоваться формулой производной произведения: 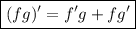$\boxed{(fg)'=f'g+fg'}$ и производной сложной функции: $\boxed{[f(g(x))]'=f'(g(x))\times g'(x)}$ .

В нашем случае: 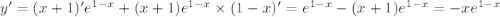$y'=(x+1)'e^{1-x}+(x+1)e^{1-x}\times (1-x)'=e^{1-x}-(x+1)e^{1-x}=-xe^{1-x}$ . Приравниваем к 0: 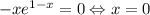$-xe^{1-x}=0 \Leftrightarrow x=0$ , так как 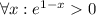$\forall x:e^{1-x}0$ . При этом если 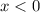, то производная положительна, а если 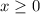$x\geq 0$ , то производная отрицательна. Значит, 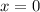x=0 — точка максимума.

Саидос

Математика

4,7(34 оценок)

Капусти 911-(198+198*2)=317

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.