Регистрация Спросить otvet5GPT
Malıw
09.05.2022 01:57
Математика
Есть ответ 👍

Докажите, что среди чисел вида 2^{n} -3 существует бесконечно много чисел, делящихся на 5, и бесконечно много чисел, делящихся на 13, но не существует ни одного числа, делящегося на 65. Указание: рассмотреть остатки от деления числа на 5 и 13

212
253
Посмотреть ответы 2

Ответы на вопрос:

tofik4
tofik4
4,8(50 оценок)

Разность чисел a и b делится на c, если a и b имеют равные остатки при делении на с.

Рассмотрим остатки от деления данного выражения на 5. 3 имеет остаток 3, поэтому 2ⁿ также должно иметь остаток 3. Заметим, что все числа вида 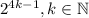2^{4k-1},k\in\mathbb{N} имеют такой остаток. Докажем это методом математической индукции:

1. База индукции: при k = 1 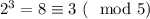2^3=8\equiv 3\ (\mod 5)

2. Переход: пусть при k = x утверждение верно. Тогда при k = x + 1:

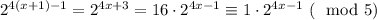
2^{4(x+1)-1}=2^{4x+3}=16\cdot2^{4x-1}\equiv 1\cdot2^{4x-1}\ (\mod 5)

Утверждение доказано. Так как k — любое натуральное число, данных в условии чисел бесконечно много.

Аналогично 2ⁿ должно иметь остаток 3 при делении на 13. Также докажем по индукции, что числа вида 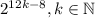2^{12k-8},k\in\mathbb{N} подходят:

1. База индукции: при k = 1 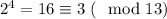2^4=16\equiv 3\ (\mod 13)

2. Переход: пусть при k = x утверждение верно. Тогда при k = x + 1:

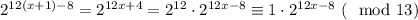
2^{12(x+1)-8}=2^{12x+4}=2^{12}\cdot2^{12x-8}\equiv 1\cdot2^{12x-8}\ (\mod 13)

Утверждение доказано, данных в условии чисел, делящихся на 13, бесконечно много.

Докажем, что не существует чисел вида 2ⁿ, которые при делении на 65 дают остаток 3. Выпишем первые 12 остатков: 2 4 8 16 32 64 63 61 57 49 33 1. Среди них нет ни одной тройки. Докажем, что они повторяются, то есть 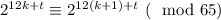2^{12k+t}\equiv 2^{12(k+1)+t}\ (\mod 65), где k — неотрицательное целое число, 0 ≤ t ≤ 11 (за исключением случая k = t = 0):

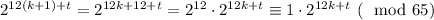2^{12(k+1)+t}=2^{12k+12+t}=2^{12}\cdot 2^{12k+t}\equiv 1\cdot 2^{12k+t}\ (\mod 65) — верно. Значит, 2ⁿ не может давать 3 при делении на 65.

SKYRIM6
SKYRIM6
4,6(90 оценок)
Представим 2500 как 100%. тогда 25% - 1/4. 1/4 от 2500 - 625 тг. 2500 -625 = 1875 (тг) ответ: книга будет стоить 1875 тг.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS