Алгебра: .............................................................................. Решить неравенство

sanelya2

15.05.2022 17:21

Алгебра

Есть ответ 👍

..............................................................................
Решить неравенство

168

416

Посмотреть ответы 2

Ответы на вопрос:

Наташа006

Алгебра

4,5(91 оценок)

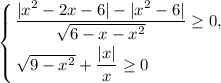
$\displaystyle \left \{ {{\dfrac{|x^{2} - 2x - 6| - |x^{2} - 6|}{\sqrt{6 - x - x^{2}} } \geq 0,} \atop {\sqrt{9 - x^{2}} + \dfrac{|x|}{x} \geq 0} \ \ \ \ \ \ \ \ \ \ \ \ \ } \right.$

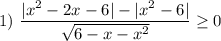
$1) \ \dfrac{|x^{2} - 2x - 6| - |x^{2} - 6|}{\sqrt{6 - x - x^{2}} } \geq 0$

Данное неравенство равносильно системе неравенств:

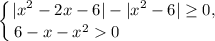
$\displaystyle \left \{ {|x^{2} - 2x - 6| - |x^{2} - 6| \geq 0,} \atop {6 - x - x^{2} 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }} \right.$

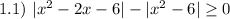
$1.1) \ |x^{2} - 2x - 6 | - |x^{2} - 6| \geq 0$

Нули модулей:

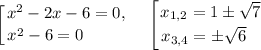
$\displaystyle \left [ {{x^{2} - 2x - 6 = 0, } \atop {x^{2} - 6 = 0 \ \ \ \ \ \ \ \, }} \right. \ \ \ \left [ {{x_{1,2} = 1 \pm \sqrt{7}} \atop {x_{3,4} = \pm \sqrt{6} \ \ \, }} \right.$

Раскроем модули на пяти участках, используя правило раскрытия модуля:

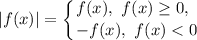
$|f(x)| = \displaystyle \left \{ {{f(x), \ f(x) \geq 0, \ \, } \atop {-f(x), \ f(x) < 0}} \right.$

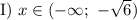
$\text{I}) \ x \in (-\infty; \ -\sqrt{6})$

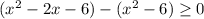
$(x^{2} - 2x - 6) - (x^{2} - 6) \geq 0$

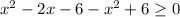
$x^{2} - 2x - 6 - x^{2} + 6 \geq 0$

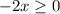
$-2x \geq 0$

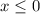
$x \leq 0$

Учитывая условие, 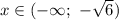$x \in (-\infty; \ -\sqrt{6})$

$\text{II}) \ x \in [-\sqrt{6}; \ 1 - \sqrt{7}]$

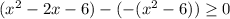
$(x^{2} - 2x - 6) - (-(x^{2} - 6)) \geq 0$

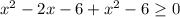
$x^{2} - 2x - 6 + x^{2} - 6 \geq 0$

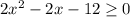
$2x^{2} - 2x - 12 \geq 0$

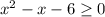
$x^{2} - x - 6 \geq 0$

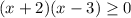
$(x + 2)(x - 3) \geq 0$

$x \in (-\infty; \ -2] \cup [3; \ +\infty)$

Учитывая условие, $x \in [-\sqrt{6}; \ -2]$

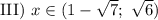
$\text{III}) \ x \in (1 - \sqrt{7}; \ \sqrt{6})$

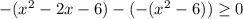
$-(x^{2} - 2x - 6) - (-(x^{2} - 6)) \geq 0$

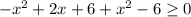
$-x^{2} + 2x + 6 + x^{2} - 6 \geq 0$

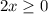
$2x \geq 0$

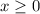
$x \geq 0$

Учитывая условие, 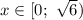$x \in [0; \ \sqrt{6})$

$\text{IV}) \ x \in [\sqrt{6}; \ 1 +\sqrt{7}]$

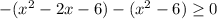
$-(x^{2} - 2x - 6) - (x^{2} - 6) \geq 0$

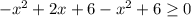
$-x^{2} + 2x + 6 - x^{2} + 6 \geq 0$

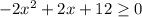
$-2x^{2} + 2x + 12 \geq 0$

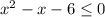
$x^{2} - x - 6 \leq 0$

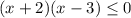
$(x + 2)(x - 3) \leq 0$

$x \in [-2; \ 3]$

Учитывая условие, $x \in [\sqrt{6}; \ 3]$

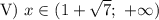
$\text{V}) \ x \in (1 + \sqrt{7}; \ +\infty)$

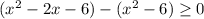
$(x^{2} - 2x - 6) - (x^{2} - 6) \geq 0$

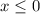
$x \leq 0$

Нет решений.

Объединим все пять случаев решения:

$x \in (-\infty; \ -2] \cup [0; \ 3]$

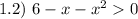
$1.2) \ 6 - x - x^{2} 0$

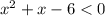
$x^{2} + x - 6 < 0$

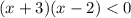
(x + 3)(x - 2)< 0

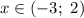
$x \in (-3; \ 2)$

Имеем:

$\displaystyle \left \{ {{x \in (-\infty; \ -2] \cup [0; \ 3]} \atop {x \in (-3; \ 2) \ \ \ \ \ \ \ \ \ \ \ \ \ \,}} \right.$

Находим пересечение решений:

$x \in (-3; \ -2] \cup [0; \ 2)$

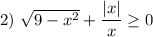
$2) \ \sqrt{9 - x^{2}} + \dfrac{|x|}{x} \geq 0$

Ограничения:

$\displaystyle \left \{ {{9 - x^{2} \geq 0,} \atop {x \neq 0 \ \ \ \ \ \ \ }} \right. \ \ \ \ \ \ \left \{ {{x \in [-3; \ 3] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \, } \atop {x \in (-\infty; \ 0) \cup (0; \ +\infty)} } \right.$

$x \in [-3; \ 0) \cup (0; \ 3]$

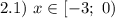
$2.1) \ x \in [-3; \ 0)$

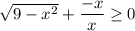
$\sqrt{9 - x^{2}} + \dfrac{-x}{x} \geq 0$

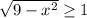
$\sqrt{9 - x^{2}} \geq 1$

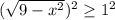
$(\sqrt{9 - x^{2}})^{2} \geq 1^{2}$

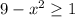
$9 - x^{2} \geq 1$

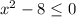
$x^{2} - 8 \leq 0$

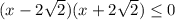
$(x - 2\sqrt{2})(x + 2\sqrt{2}) \leq 0$

$x \in [-2\sqrt{2}; \ 2\sqrt{2}]$

Учитывая условие, 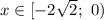$x \in [-2\sqrt{2}; \ 0)$

$2.2) \ x \in (0; \ 3]$

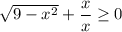
$\sqrt{9 - x^{2}} + \dfrac{x}{x} \geq 0$

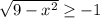
$\sqrt{9 - x^{2}} \geq -1$

$x \in (0; \ 3]$

Объединяем решения:

$x \in [-2\sqrt{2}; \ 0) \cup (0; \ 3]$

Получили решения обоих неравенств в системе неравенств:

$\displaystyle \left \{ {{x \in (-3; \ -2] \cup [0; \ 2) \ \, } \atop {x \in [-2\sqrt{2}; \ 0) \cup (0; \ 3]}} \right.$

Находим пересечение решений:

$x \in [-2\sqrt{2}; \ -2] \cup (0; \ 2)$

ответ: $x \in [-2\sqrt{2}; \ -2] \cup (0; \ 2)$

vika2063

Алгебра

4,6(44 оценок)

Пусть х раб/час - производительность 2го рабочего, тогда раб/час - производительность 1го рабочего. из условия об их совместной работе следует уравнение 0,025 раб/час - производительность 2го рабочего ⇒ самостоятельно он выполняет всю работу за 1: 0,025=40 часов. раб/час - производительность 1го рабочего ⇒ самостоятельно он выполняет всю работу за 1: (1/90)=90 часов.ответ: 40ч и 90ч

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

nucubidzezura
01.10.2021 06:23

Розкласти на множники, розв язати до 16.04, алгебра, 8 клас...
JeDor15
24.02.2021 07:24

человеку который всё забыл на самоизоляции))) EF = ED; ∠DFE =...
Dianakuharur2
19.05.2022 00:00

1)2sin22°30 *cos7°30 2)2cos7°30 *sin52°30 3)cos п/4*cos п/12 4)sin...
jahinanaily
18.04.2023 00:51

3. Яку суму треба внести на депозит д о о річних,щоб одержати...
carrot4
28.07.2020 16:56

При каких значениях параметра a уравнение имеет одно решение?...
Dag18y5557hvvhi
30.01.2020 21:03

Нужно применить формулу квадрата разности и вычислить 8,97 в 2...
31752
25.05.2020 04:07

Сколько будет а) 1,2 3ст*5 3ст б) (-2) 3ст - (-3) 4 ст...
anastasia8879
27.01.2021 09:27

Вынесите за скобки общий множитель: 40b²x²+10bx³-110b²x...
vadimtolpegin
12.06.2022 00:53

Решите уравнение: (2x-3)×(5x+2)-x(3-2x)=0...
andreyglukhov7
21.02.2021 02:54

(4x+28)*1,2+1,3*(x+3)+(-1,7-6,1x)=35,8...

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.