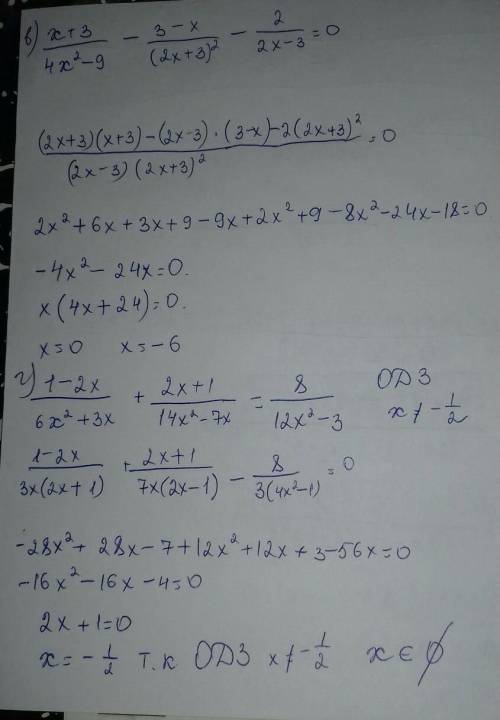Регистрация Спросить otvet5GPT
АуTист
29.08.2021 14:55
Алгебра
Есть ответ 👍

ОЧЕНЬ РЕШИТЕ ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ. задачки:В Г.​

137
182
Посмотреть ответы 3

Ответы на вопрос:

durindub007
durindub007
4,6(50 оценок)

Объяснение:

☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆


ОЧЕНЬ РЕШИТЕ ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ. задачки:В Г.​
ДИЛЯ2002111
ДИЛЯ2002111
4,7(76 оценок)

Объяснение:

в)  (x + 3)/*((2x - 3)(2x + 3))  -  (3 - x)/((2x + 3)^2) - 2/(2x - 3) = 0

(2x ^2 + 3x + 6x + 9 - 6x + 2x^2 + 9 - 3x - 8x^2 - 24x - 18)/((2x - 3)(2x + 3)^2) =

= (- 4x^2 - 24x)/((2x - 3)(2x + 3)^2)

Уравнение равно нулю, если числитель равен нулю

- 4x^2 - 24x = 0  |: (-4)

x^2 + 6x = 0

x(x + 6) = 0

x = 0

x = - 6

г) ОДЗ   2x ± 1 ≠ 0

x ≠ ± 0,5

x ≠ 0

(1 - 2x)/(3x(2x + 1)) + (2x + 1)/(7x(2x - 1)) - 8/(3(2x - 1)(2x + 1)) = 0

(14x - 28x^2 - 7 + 14x + 12x^2 + 6x +6x + 3 - 56x)/(21x(2x - 1)(2x + 1)) =

= (-16x^2 - 16x - 4)/(21x(2x - 1)(2x + 1))

Уравнение равно нулю, если числитель равен нулю

-16x^2 - 16x - 4 = 0  | : (-4)

4x^2 + 4x + 1 = 0

(2x + 1)^2 = 0

x = -0,5 - ∅ (ОДЗ)

ответ - решения нет

кошачка278
кошачка278
4,7(89 оценок)

f(x)=\frac{1}{x+sinx}\; \; ,\quad (\frac{1}u})'=-\frac{u'}{u^2}'(x)=-\frac{(x+sinx)'}{(x+sinx)^2}=-\frac{1+cosx}{(x+sinx)^2}''(x)=-\frac{-sinx(x+sinx)^2-(1+cosx)\cdot 2(x+sinx)\cdot (1+cosx)}{(x+sinx)^4}=\frac{sinx\cdot (x+sinx)+2\cdot (1+cosx)^2}{(x+sinx)^3}'''(x)=\frac{1}{(x+sinx)^3}\cdot \big [\big (cosx(x+sinx)+sinx(1+cosx)--4(1+cosx)\cdot sinx\big )(x+sinx)^3-\big (sinx\cdot (x+sinx)+2\cdot (1+cosx)^2\big )\times 3(x+sinx)^2\cdot (1+cosx)\big ]

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS