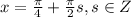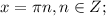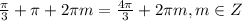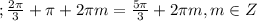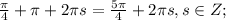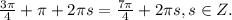Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
У начальника N рублей, каждому работнику выплачивает по 30.000 рублей,количество...
 maria2005dp01.09.2021 13:18
maria2005dp01.09.2021 13:18 -
Устройство состоит из 1000 элементов, работающих независимо друг...
 Shirimi22.05.2022 01:08
Shirimi22.05.2022 01:08 -
решить! алгебра 9 класс....
 sofya11223308.06.2020 00:23
sofya11223308.06.2020 00:23 -
Если 9% от числа а равны 109% от числа б, то отношение а/б равно...
 Korish200510.09.2021 22:53
Korish200510.09.2021 22:53 -
{x-y=0 {x-3y=6 решить способом подстановкии...
 hjdbr03.10.2020 11:48
hjdbr03.10.2020 11:48 -
Втреугольнике мрq mq=14, sin угла mpq=0,5. найдите радиус описанной...
 gasanova68315.08.2021 08:58
gasanova68315.08.2021 08:58 -
Сколькими способами можно разделить группу дежурных из 17 учащихся,...
 Dasha55551111106.11.2022 21:27
Dasha55551111106.11.2022 21:27 -
Докажите что последовательность натуральных чисел которые при делении...
 КристинаВощевоз5413.09.2021 14:09
КристинаВощевоз5413.09.2021 14:09 -
Розвяжіть додавання ситему рівнянь {5x+2y=25. {3x+4y=29....
 def0456513.01.2020 01:27
def0456513.01.2020 01:27 -
Представьте многочлен в виде произведения: 2a - ac - 2c + c²...
 beynyadima07.01.2023 19:20
beynyadima07.01.2023 19:20

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

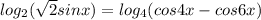
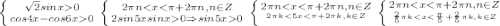
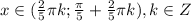
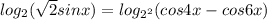
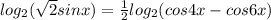
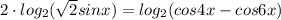
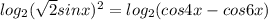
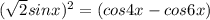
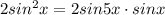
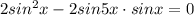

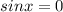 или sinx-sin5x=0
или sinx-sin5x=0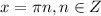 или
или 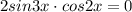 ⇒
⇒ 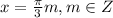 или
или