Регистрация Спросить otvet5GPT
AINASH751212
04.01.2023 20:05
Математика
Есть ответ 👍

Т3) Сколько корней имеет уравнение |cosx| + корень(sin2x) =0 на отрезке [0; 2пи] Заранее большое

238
243
Посмотреть ответы 2

Ответы на вопрос:

Артем222211
Артем222211
4,5(28 оценок)

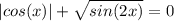
|cos(x)| + \sqrt{sin(2x)} = 0

Можно решить двумя Рассмотрим первый:

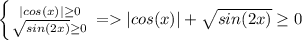
\left \{ {{|cos(x)| \geq 0} \atop {\sqrt{sin(2x)}\geq 0 }} \right. = |cos(x)| + \sqrt{sin(2x)} \geq 0

Исходя из этого понимаем, что выражение равно нулю только в том случае, если оба неотрицательных слагаемых равны нулю:

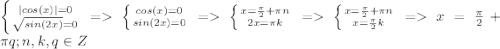
\left \{ {{|cos(x)| = 0} \atop {\sqrt{sin(2x)} = 0}} \right. = \left \{ {{cos(x) = 0} \atop {sin(2x) = 0}} \right. = \left \{ {{x = \frac{\pi}{2} + \pi n } \atop {2x = \pi k}} \right. = \left \{ {{x = \frac{\pi}{2} + \pi n } \atop {x = \frac{\pi}{2} k}} \right. = x = \frac{\pi}{2} + \pi q; n, k, q \in Z

ответ: 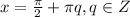x = \frac{\pi}{2} + \pi q, q \in Z

Второй

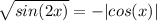
\sqrt{sin(2x)} = -|cos(x)|\\

Данное уравнение равносильно следующей системе:

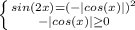
\left \{ {{sin(2x) = (-|cos(x)|)^2} \atop {-|cos(x)| \geq 0}} \right.

Так как 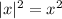|x|^2 = x^2, то:

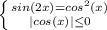
\left \{ {{sin(2x) = cos^2(x)} \atop {|cos(x)| \leq 0}} \right.

Модуль - это число неотрицательное. А это значит, что неравенство системы имеет смысл только тогда, когда cos(x) = 0:

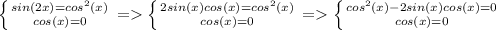
\left \{ {{sin(2x) = cos^2(x)} \atop {cos(x) = 0}} \right. = \left \{ {{2sin(x)cos(x) = cos^2(x)} \atop {cos(x) = 0}} \right. = \left \{ {{cos^2(x) - 2sin(x)cos(x) = 0} \atop {cos(x)=0}} \right.

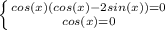
\left \{ {{cos(x)(cos(x)-2sin(x)) = 0} \atop {cos(x) = 0}} \right.

Первое уравнение системы, очевидно, имеет решение cos(x) = 0. ответ получаем тот же.

ответ: 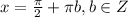x = \frac{\pi}{2} + \pi b, b \in Z

hffyj95
hffyj95
4,7(31 оценок)
1) 40*2=80 2) 80-12=68 ответ: 68

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS