Регистрация Спросить otvet5GPT
skalli05
01.10.2022 03:50
Математика
Есть ответ 👍

Решите подробно систему уравнений.

292
292
Посмотреть ответы 3

Ответы на вопрос:

anastasiykucher
anastasiykucher
4,6(18 оценок)

1

Пошаговое объяснение:

система має лише один корінь, тобто "одно решение"


Решите подробно систему уравнений.
kakaxa6
kakaxa6
4,6(36 оценок)

ответ: 1 решение

Пошаговое объяснение:

Первый аналитический)

Данная система эквивалентна уравнению :

3^(-x) =|x+2|

3^(-x) -|x+2| = 0

3^(-x) +-(x+2) = 0   , в зависимости от знака выражения x+2

Найдем производную  f(x) = 3^(-x) +-(x+2)

f'(x) = -3^(-x) *ln(3) +-1

1)  x+2 >=0

f'(x)= -3^(-x) *ln(3) -1 <= 0  - функция монотонно убывает

2)  x+2<0 ;  x<-2

 f'(x) = -3^(-x) *ln(3) +1

 При  x<-2  ;  -x > 2  ⇒ -3^(-x) <- 3^2 = -9

Поскольку :  3>e , то ln(3) >1 ⇒ -3^(-x) *ln(3)  < -9 ⇒ -3^(-x) *ln(3) +1  <- 8 - функция монотонно убывает.

Вывод :  Данная система эквивалентна уравнению :

3^(-x) =|x+2|

3^(-x) -|x+2| = 0

3^(-x) +-(x+2) = 0   , в зависимости от знака выражения x+2

Найдем производную  f(x) = 3^(-x) +-(x+2)

f'(x) = -3^(-x) *ln(3) +-1

1)  x+2 >=0

f'(x)= -3^(-x) *ln(3) -1 <0  - функция монотонно убывает

2)  x+2<0 ;  x<-2

 f'(x) = -3^(-x) *ln(3) +1

 При  x<-2  ;  -x > 2  ⇒ -3^(-x) <- 3^2 = -9

Поскольку :  3>e , то ln(3) >1 ⇒ -3^(-x) *ln(3)  < -9 ⇒ -3^(-x) *ln(3) +1  <- 8 - функция монотонно убывает.

Вывод :  функция монотонно убывает на множестве действительных чисел .

Заметим, что  f(-1) = 3^1 -|1| = 2>0 ;  f(0)= 3^0 -|2| = 1-2 =-1<0

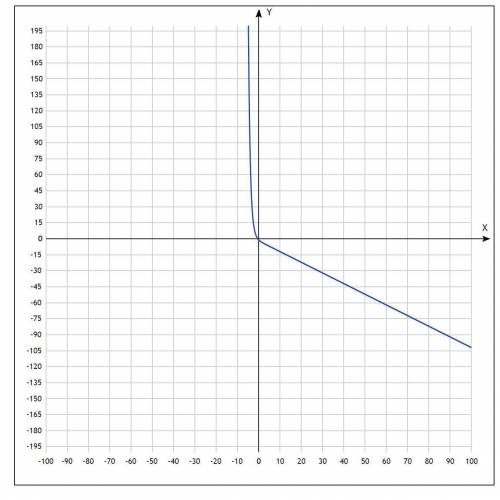
Данная функция может иметь горизонтальные ассимптоты, однако, поскольку функция монотонно убывает на множестве действительных чисел, то может иметь не более одной ассимптоты  при  возрастании  аргумента и не более одной ассимптоты  при убывании аргумента. Таким образом, поскольку f(-1) >0  и f(0) < 0   и функция монотонно убывает на множестве действительных чисел, уравнение

3^(-x) -|x+2| = 0  имеет единственное решение, которое лежит на промежутке x∈(-1;0), как  и представленная система уравнений.

На рисунке 1 показан график функции f(x).

Второй аналитически-графический)

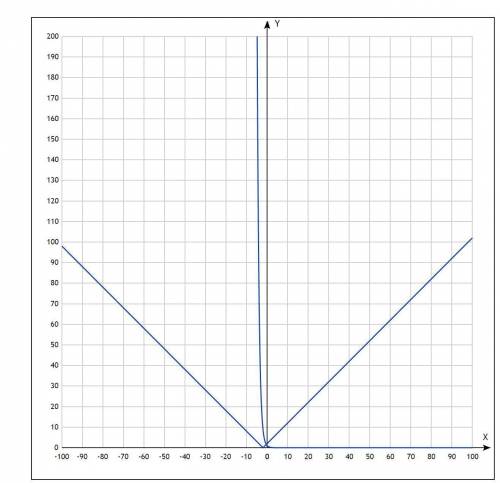
На рисунке 2 показаны графики функций: y= 1/3^x = 3^(-x) и |x+2| в одной системе координат.  В силу геометрических соображений при построении графиков, очевидно, что  правая ветка модуля точно пересекает график степенной функции и ровно в одной точке. Таким образом одно решение уже существует.

Так же , но уже менее очевидно, левая ветка модуля не пересекает степенную функцию. Это  необходимо доказать.

Докажем, что  при любом x<-2 (область определения левой ветки модуля) степенная функция больше чем левая ветка модуля, то есть :

f(x) =3^(-x) - (-x-2) >= 0

Доказать это можно двумя

1) Интуитивно :  

f(-2) =  3^2  -|0| = 9 >0

Из графика видно , что при убывании аргумента  от -2  оба графика возрастают, но при этом степенная функция растет быстрее линейной, то есть f(x) > 9 , то есть левая ветка модуля не пересекает степенную функцию.

Вывод : cистема имеет единственное решение.

2)  Cтрого.

Cкорость роста линейной функции при УБЫВАНИИ аргумента на x<-2 (-x-2) постоянна  и

равна u= -(-x-2)' = 1

А у показательной функции скорость увеличивается  :

v = -(3^(-x) )' = 3^(-x)* ln(3)> 9*ln(3) > u  , при  x<-2.

Тогда, поскольку f(-2)= 9 > 0 , то степенная функция больше линейной при x<-2


Решите подробно систему уравнений.
Решите подробно систему уравнений.
Волна1610
Волна1610
4,8(56 оценок)

Відповідь:

число 20

Покрокове пояснення: 14 +18 = 32

52-32=20))

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS