Регистрация Спросить otvet5GPT
tmihailviktoroozvxn9
11.01.2023 06:39
Геометрия
Есть ответ 👍

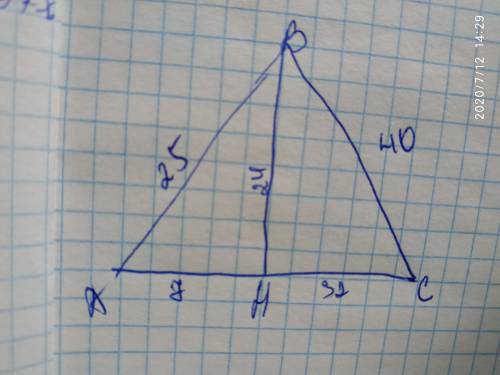
У трикутнику із сторонами 25 і 40 см з вершини кута між ними проведено висоту, яка ділить третю його сторону на відрізки, менший з яких дорівнює 7 см. Обчисліть периметр трикутника.

285
296
Посмотреть ответы 3

Ответы на вопрос:

Duka2003
Duka2003
4,7(50 оценок)

104 см

Объяснение:

Дано

Трикутник ∆АВС

АВ=25 см

ВС=40 см

АН=7

ВН=? висота

АС=? сторона трикутника

Р∆АВС=? периметр трикутника

Рішення.

∆АВН прямокутний, ВН і АН - катети.

АВ- гіпотенуза.

За теоремою Піфагора знайдемо ВН

ВН²=АВ²-АН²=25²-7²=625-49=576 см

ВН=√576=24 см.

∆ВНС- прямокутний, ВН і НС - катети, ВС- гіпотенуза.

За теоремою Піфагора знайдемо НС

НС²=ВС²-ВН²=40²-24²=1600-576=1024 см

НС=√1024=32 см

АС=АН+НС=7+32=39 см

Р∆АВС=АВ+ВС+АС=25+40+39=104 см периметр трикутника.

Відповідь: периметр трикутника дорівнює 104 см


У трикутнику із сторонами 25 і 40 см з вершини кута між ними проведено висоту, яка ділить третю його
динка84
динка84
4,5(97 оценок)

ответ:104 см

Объяснение:

Пусть треугольник АВС.   АВ=25 см ,  ВС=40 см,  ВН (высота)=?,

АН=7см

Из треугольника АВН по т Пифагора найдем ВН.

ВН= sqrt (AB^2- AH^2)=sqrt(625-49)=24 см

Тогда из треугольника ВНС по т Пифагора находим НС=sqrt(BC^2-BH^2)

HC=sqrt(1600-576)=sqrt(1024)=32

AC=HC+AH=7+32=39 см

P=25+40+39=104 см

070974zZ
070974zZ
4,6(33 оценок)

ответ:

объяснение:

доклад тригонометрии кратко сообщение

создания тригонометрии плотно связанна с космосом, а точнее с решением астрономических . изначально на первых этапах развития этого направление в были положены в основу примитивные соотношение длин и сторон треугольника. но со временем она развивалось и превратилось в сегодняшний вариант этого раздела. сейчас это небольшой раздел , который включают в себя лишь некоторые программы обучения. если взять современную , то тригонометрия это узкий раздел, изучающий взаимоотношения углов треугольника.

изначально этот раздел не имел общего названия, а все древние называли тригонометрию по-своему. впервые понятия «тригонометрия» было обнаружено в 1505 году в научной работе ученого питискуса. сам термин был родом из древнегреческого языка и при дословном переводе означал «измеряю углы треугольника». речь об измерении, здесь употребляется в переносном смысле, то есть не буквальное измерение углов, а нахождение их при формул и известных элементов.      

когда в руках оказались древние рукописи и манускрипты они смогли сделать несколько заключений. они пришли к выводу, что основателем тригонометрии был древнегреческий и астроном гипарх. в ходе своих научных работ он стал задумываться о новаторских способах решения треугольника.   гипарх был удивительным   ученым своего времени, так как он смог создать начальный уровень современной тригонометрии, живя в втором веке до нашей эры. также в это время жил и творил пифагор, который смог создать правильное соотношения сторон прямоугольного треугольника, то есть теорему пифагора.

 

значительный вклад в тригонометрию внесли молодые ученые из индии, но эти открытия были сделаны уже в средневековые времена. также в эпоху средневековья были сделаны множества различных открытий и других направлениях науки, культуры и общества.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS