Физика: 3 задачи Всё на скрине

Diana2004250

11.11.2021 11:50

Физика

Есть ответ 👍

3 задачи Всё на скрине

187

496

Посмотреть ответы 2

Ответы на вопрос:

yaltame

Физика

4,8(24 оценок)

Попытаюсь решить.

1. Сразу ясно, что частица находится в параболической потенциальной яме, в таких условиях она является гармоническим осциллятором.

Функция Лагранжа для такой частицы

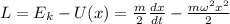
$L=E_k-U(x)=\frac{m}{2}\frac{dx}{dt}-\frac{m\omega ^2x^2}{2}$

Уравнение Эйлера-Лагранжа

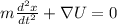
$m\frac{d^2x}{dt^2}+\nabla U=0$

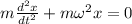
$m\frac{d^2x}{dt^2}+m\omega^2x=0$

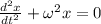$\frac{d^2x}{dt^2}+\omega^2x=0$ - классическое уравнение гармонического осциллятора, о чем было сказано в начале.

Его общее решение

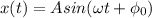
$x(t)=Asin(\omega t+\phi_0)$

Решим задачу Коши для указанных условий (примем начальную фазу для простоты за ноль)

1) Начальное положение частицы - положение равновесия, но есть отличная от нуля начальная скорость 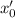x_0'

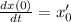
$\frac{dx(0)}{dt} =x_0'$

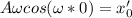
$A\omega cos(\omega *0)=x'_0$

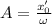
$A=\frac{x_0'}{\omega}$

Частное решение 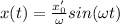$x(t)=\frac{x_0'}{\omega}sin(\omega t)$

2) Здесь наоборот, частица выведена из положения равновесия, но не имеет начальной скорости, значит амплитуда сходу будет равна 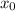x_0 , а частное решение будет иметь вид

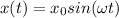
$x(t)=x_0sin(\omega t)$

2) Момент инерции вычисляется как интеграл следующего вида

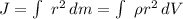
$J=\int\ {r^2} \, dm=\int\ {\rho r^2} \, dV$

Где dV - объем цилиндрического коаксиального слоя толщиной dr

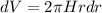
$dV=2\pi Hrdr$

Окончательно

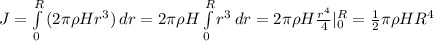
$J=\int\limits^R_0 {(2\pi\rho Hr^3)} \, dr= 2\pi \rho H \int\limits^R_0 {r^3} \, dr =2\pi \rho H \frac{r^4}{4}|_0^R=\frac{1}{2}\pi \rho HR^4$

Центростремительное ускорение по внешнему радиусу тора должно совпасть с g₀

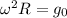
$\omega ^2R=g_0$

Требуемая угловая частота вращения

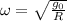
$\omega=\sqrt{\frac{g_0}{R} }$

Период обращения

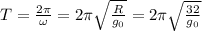
$T=\frac{2\pi }{\omega} =2\pi \sqrt{\frac{R}{g_0} }=2\pi \sqrt{\frac{32}{g_0} }$

Частота обращения

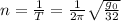$n=\frac{1}{T}=\frac{1}{2\pi } \sqrt{\frac{g_0}{32} }$ .

rudens2007

Физика

4,7(53 оценок)

D= 2.5 * 10-5 мм = 2.5 * 10-8 мs = v/d =1м3 / 2.5 * 10-8 м =4*10^7 м2

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Физика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.