Регистрация Спросить otvet5GPT
fanfa
02.01.2022 05:59
Алгебра
Есть ответ 👍

Решите неравенство............

255
362
Посмотреть ответы 2

Ответы на вопрос:

Юлия34567
Юлия34567
4,7(21 оценок)

Применяя метод рационализации получаем систему:

{ctgx >0⇒ x∈ (πm; (π/2)+πm), m∈Z

{(1+sinx)/(1-cosx) >0⇒  x≠(-π/2)+2πk, x≠2πn, k, n ∈Z

{(ctgx-1)·((1+sinx)/(1-cosx)  - ctgx ) <0

Решаем третье неравенство системы:

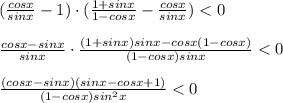
(\frac{cosx}{sinx}-1)\cdot (\frac{1+sinx}{1-cosx} - \frac{cosx}{sinx})

Решаем методом интервалов.

Находим нули числителя:

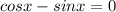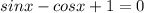cosx-sinx=0    или        sinx-cosx+1=0    вводим вс угол

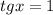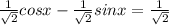
tgx=1                   или      \frac{1}{\sqrt{2}} cosx-\frac{1}{\sqrt{2}}sinx=\frac{1}{\sqrt{2}}

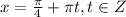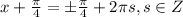x=\frac{\pi }{4} +\pi t, t\in Z   или     x+\frac{\pi }{4}=\pm\frac{\pi }{4}+2 \pi s, s\in Z  не входят в ОДЗ

Находим нули знаменателя:

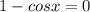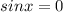
1-cosx=0         или    sinx=0

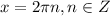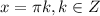
x=2\pi n, n\in Z    или  x=\pi k, k \in Z

(0) __+__ (π/4)___-__ (π/2)

При х=π/6

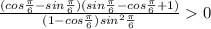
\frac{(cos\frac{\pi }{6} -sin\frac{\pi }{6})(sin\frac{\pi }{6}-cos\frac{\pi }{6}+1)}{(1-cos\frac{\pi }{6})sin^2\frac{\pi }{6}} 0

При х=π/3

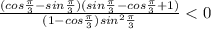
\frac{(cos\frac{\pi }{3} -sin\frac{\pi }{3})(sin\frac{\pi }{3}-cos\frac{\pi }{3}+1)}{(1-cos\frac{\pi }{3})sin^2\frac{\pi }{3}}

О т в е т.( (π/4)+πn; (π/2)+πn), n∈Z

McBlanse
McBlanse
4,4(91 оценок)
2а/(а-в-с)=2а/(а-(в+с)=2*3/(3-15)=6/-12=-1/2 у+5у=6у у любое число 4/(5(3-d))          d≠3             d∈(-∞; 3)∪(3; +∞) 3d/(2(3d-7))        d≠2 1/3          d∈(-∞; 2 1/3)∪(2 1/3; +∞) 6у – (2у – (4у – (2 - =6у-(2у-(4у-2+у))=6у-(2у-4у+2-у)=6у-2у+4у-2+у=9у-2

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS