1) Докажите, что при любом натуральном n число 21^n + 4^(n+2) делится на 17 2)Найти последние две цифры числа 7^302
186
326
Ответы на вопрос:
1) 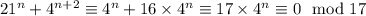
2) требуется вычислить 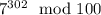 . По модулю 25:
. По модулю 25: 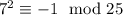 , поэтому
, поэтому 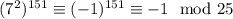 . По модулю 4:
. По модулю 4: 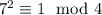 , поэтому
, поэтому 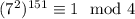 . По китайской теореме об остатках решение единственно по модулю
. По китайской теореме об остатках решение единственно по модулю 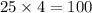 и равно
и равно 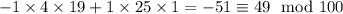 (результат прямого применения теоремы). Итак, число оканчивается на 49
(результат прямого применения теоремы). Итак, число оканчивается на 49
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Пари чисел (х1, у1) і (х2, у2) є розв язками системи рівнянь у-х=2 та...
 zdiana108.10.2020 20:49
zdiana108.10.2020 20:49 -
Самостійна робота 7 клас алгебра...
 kostya79bat112.12.2020 09:19
kostya79bat112.12.2020 09:19 -
Во всех подъездах дома одинаковое число этажей, а на каждом этаже одинаковое...
 alinaozhiganova02.09.2022 11:21
alinaozhiganova02.09.2022 11:21 -
Назовите больший корень уравнения: 5kx+7=5(3x-4)...
 Aisulu12345613.01.2020 08:09
Aisulu12345613.01.2020 08:09 -
Поясніть будь ласка як це робити. Номер завдання 367....
 Умникзаумник103.10.2020 22:34
Умникзаумник103.10.2020 22:34 -
log2 32 + ln e - lg100...
 niketa77720.06.2020 10:14
niketa77720.06.2020 10:14 -
Реши уравнение х^2+4х+|х+3|+3=0...
 ВелмаУмница22.08.2021 01:31
ВелмаУмница22.08.2021 01:31 -
1. a) При каком условии неполное квадратное уравнение не имеет корней?...
 dashadasha2239926.08.2021 14:33
dashadasha2239926.08.2021 14:33 -
вычислить номер 1, а номер 2 внести множитель под знак корня, 3 номер...
 tayatoadvel25.05.2021 02:25
tayatoadvel25.05.2021 02:25 -
Решите уравнение: 2sin-✓3=0...
 WaysWhite06.04.2021 01:28
WaysWhite06.04.2021 01:28

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
