Математика: Исследовать ряды на сходимость

vlada041104

22.04.2022 09:45

Математика

Есть ответ 👍

Исследовать ряды на сходимость

172

402

Посмотреть ответы 2

Ответы на вопрос:

darkhanio

Математика

4,4(21 оценок)

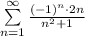
$\sum\limits^{\infty}_{n=1}\frac{(-1)^n\cdot 2n}{n^2+1}$

Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется

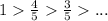
$1\frac{4}{5}\frac{3}{5}...$

По второму признаку Лейбница предел ряда должен стремится к 0.

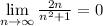
$\lim\limits_{n\to \infty}\frac{2n}{n^2+1}=0$

Таким образом, рассматриваемый ряд сходится. Теперь нужно исследовать на абсолютной и условной сходимости ряда. Возьмём данный ряд по модулю

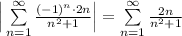$\Big|\sum\limits^\infty_{n=1}\frac{(-1)^n\cdot 2n}{n^2+1}\Big|=\sum\limits^\infty_{n=1}\frac{2n}{n^2+1}$ - расходящийся ряд, поскольку 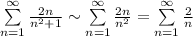$\sum\limits^\infty_{n=1}\frac{2n}{n^2+1}\sim\sum\limits^\infty_{n=1}\frac{2n}{n^2}=\sum\limits^\infty_{n=1}\frac{2}{n}$ - гармонический ряд расходится. Следовательно, данный ряд сходится условно.

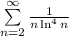
$\sum\limits^\infty_{n=2}\frac{1}{n\ln^4n}$

По интегральному признаку:

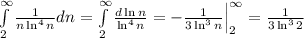
$\int \limits^\infty_2\frac{1}{n\ln^4n}dn=\int \limits^\infty_2\frac{d\ln n}{\ln^4n}=-\frac{1}{3\ln^3n}\Big|^\infty_2=\frac{1}{3\ln^32}$

Несобственный интеграл сходится, а значит сходится и рассматриваемый ряд

ахпхпха

Математика

4,5(27 оценок)

ответ:

1800

пошаговое объяснение:

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.