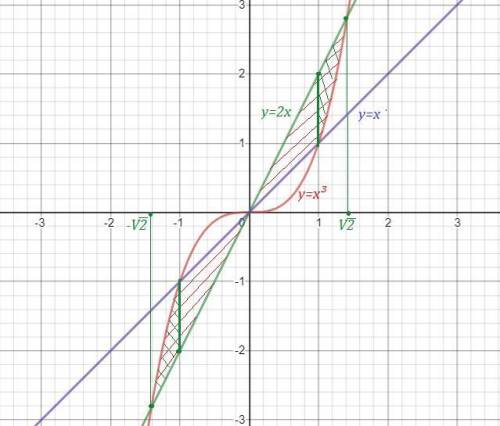
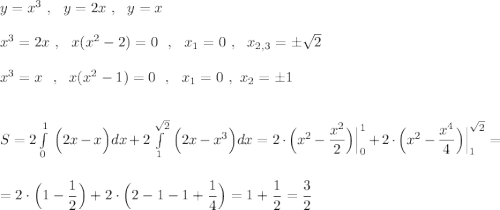Регистрация Спросить otvet5GPT
Kirillsharko
07.01.2021 01:54
Алгебра
Есть ответ 👍

Найдите площадь фигуры, ограниченной линиями y = x^3, y = 2x, y = x

263
417
Посмотреть ответы 3

Ответы на вопрос:

harchuk181002
harchuk181002
4,5(52 оценок)

y=x^3\ ,\ \ y=2x\ ,\ \ y=x\\\\x^3=2x\ ,\ \ x(x^2-2)=0\ \ ,\ \ x_1=0\ ,\ \ x_{2,3}=\pm \sqrt2\\\\x^3=x\ \ ,\ \ x(x^2-1)=0\ \ ,\ \ x_1=0\ ,\ x_2=\pm 1\\\\\\S=2\int\limits^1_0\, \Big(2x-x\Big)dx+2\int\limits^{\sqrt2}_1\, \Big(2x-x^3\Big)dx=2\cdot \Big(x^2-\dfrac{x^2}{2}\Big)\Big|_0^1+2\cdot \Big(x^2-\dfrac{x^4}{4}\Big)\Big|_1^{\sqrt2}=\\\\\\=2\cdot \Big(1-\dfrac{1}{2}\Big)+2\cdot \Big(2-1-1+\dfrac{1}{4}\Big)=1+\dfrac{1}{2}=\dfrac{3}{2}


Найдите площадь фигуры, ограниченной линиями y = x^3, y = 2x, y = x
Пава1305
Пава1305
4,5(39 оценок)

Объяснение: смотрите график и решение во вложении


Найдите площадь фигуры, ограниченной линиями y = x^3, y = 2x, y = x
Найдите площадь фигуры, ограниченной линиями y = x^3, y = 2x, y = x
МсПолинэ
МсПолинэ
4,6(96 оценок)
Sin^2 x + 2 sin (π - x) * cos x - 3 cos^2 (2π - x) = 0sin² x + 2 sin x * cos x - 3 cos² x = 0  пояснение: sin (pi - x) = sin x   cos² (2pi - x) = cos² x sin² x + 2 sin x *  cos x - 3 cos² x = 0   | : cos²x  ≠ 0 tg² x + 2 tg x - 3 = 0   вводим замену   tg x = t решаем квадратное уравнение t² + 2t - 3 = 0 d = b² - 4ac = 2² - (-4*1*3) = 4 + 12 = 16   √d = 4 t1 = (-2+4)/2 = 1 t2 = (-2-4)/2 = -3 tg x = t 1) tg x = 1  x = pi/4 + pik, k  ∈ z 2) tg x = -3 x = -arctg3 + pik, k  ∈ z ответ: pi/4 + pik, k  ∈  z; -arctg3 + pik, k  ∈ z

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS