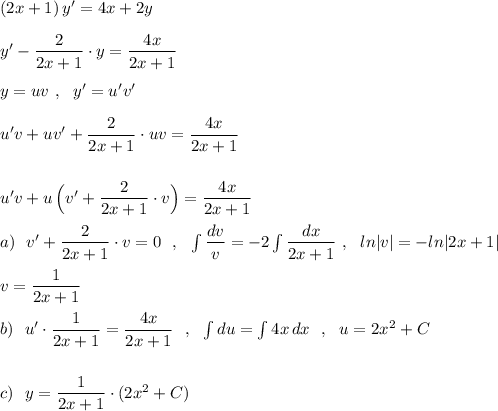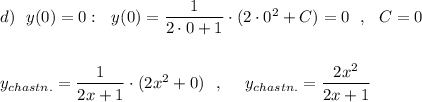Найти частное решение линейного дифференциального уравнения первого порядка, удовлетворяющего начальному условию

253

338

Посмотреть ответы 2

Ответы на вопрос:

fcnhff7

Алгебра

4,8(89 оценок)

$(2x+1)\, y'=4x+2y\\\\y'-\dfrac{2}{2x+1}\cdot y=\dfrac{4x}{2x+1}\\\\y=uv\ ,\ \ y'=u'v \uv'\\\\u'v +uv'+\dfrac{2}{2x+1}\cdot uv=\dfrac{4x}{2x+1}\\\\\\u'v+u\, \Big(v'+\dfrac{2}{2x+1}\cdot v\Big)=\dfrac{4x}{2x+1}\\\\a)\ \ v'+\dfrac{2}{2x+1}\cdot v=0\ \ ,\ \ \int \dfrac{dv}{v}=-2\int \dfrac{dx}{2x+1}\ ,\ \ ln|v|=-ln|2x+1|\\\\v=\dfrac{1}{2x+1}\\\\b)\ \ u'\cdot \dfrac{1}{2x+1}=\dfrac{4x}{2x+1}\ \ ,\ \ \int du=\int 4x\, dx\ \ ,\ \ u=2x^2+C\\\\\\c)\ \ y=\dfrac{1}{2x+1}\cdot (2x^2+C)$

$d)\ \ y(0)=0:\ \ y(0)=\dfrac{1}{2\cdot 0+1}\cdot (2\cdot 0^2+C)=0\ \ ,\ \ C=0\\\\\\ y_{chastn.}=\dfrac{1}{2x+1}\cdot (2x^2+0)\ \ ,\ \ \ \ y_{chastn.}=\dfrac{2x^2}{2x+1}$

lol1039

Алгебра

4,5(92 оценок)

А)а-по + 3 б)в-по +17 в)с-по + 10 г)d-по + 10

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

катя4802
29.06.2020 01:28

Постройте график функции. y = 3(x-5) в квадрате...
Анюся1
23.04.2021 14:43

Преобразуйте выражение в многочлен...
12Go12
31.03.2021 08:32

Является ли пара чисел (−9; 3) решением данной системы уравнений? 2x+11y=15...
kilala00
11.09.2020 09:38

На какие числа делится число 90...
lena2078
14.04.2021 12:42

Пацанчики, тут с уравнениями. (x^2-3x-4)*(x^2+x-2)...
НяшаАнька
02.07.2021 17:35

Расскажите все про линейную функцию!...
fatimatangatar
15.05.2022 13:05

Укажите решение неравенства: 3/7...
nika55551
30.03.2020 16:02

Рашите по формуле: f=k*g1*g2/r^2f=0,027 r=2000 g1=0,006 k=9*10^9 g1-?...
ПрофессорЧерепашка
27.07.2021 12:22

Найти площадь фигуры, ограниченной линиями y = x+1 и y = 3+ 2x − x^2(икс...
anfisachupina85
08.04.2021 18:02

Решить неравенство x(x+3)^3(x+4)^4(x+5)^5 =0...

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.