Найти площадь фигуры, ограниченной параболами y=4-x^2 , y=(x-2)^2 с осью Ox

173

380

Посмотреть ответы 2

Ответы на вопрос:

filip198585

Математика

4,6(80 оценок)

Пошаговое объяснение:

y₁=4-x²; y₂=(x-2)²; у = 0;

площадь фигуры - это определенный интеграл вида

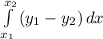
$\int\limits^{x_2}_{x_1} {(y_1 - y_2)} \, dx$

найдем х₁ и х₂. это точки пересечения графиков у₁ и у₂

4-х² = (х-2)²; 4x² -x² - x² - 4x + 4; -2x² + 4x = 0

-2x(x-2) = 0 ⇒ х₁=0; х₂=2; - это пределы интегрирования

считаем интеграл

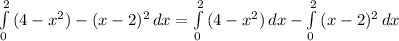
$\int\limits^2_0 {(4-x^2) -(x-2)^2} \, dx = \int\limits^2_0 {(4-x^2) } \, dx - \int\limits^2_0 {(x-2)^2} \, dx$

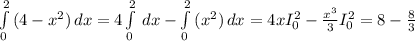
$\int\limits^2_0 {(4-x^2) } \, dx =4 \int\limits^2_0 { } \, dx - \int\limits^2_0 {(x^2) } \, dx=4xI_0^2 - \frac{x^3}{3}I_0^2 = 8 -\frac{8}{3}$

$\int\limits^2_0 {(x-2)^2} \, dx = \left[\begin{array}{ccc}u = x-2; du = dx\\x_1=0-2 = -2\\x_2=2-2=0\end{array}\right] = \int\limits^0_{-2} {u^2} \, du = \frac{u^3}{3} I_{-2}^0 = -\frac{8}{3}$

$\int\limits^2_0 {(4-x^2) -(x-2)^2} \, dx = 8-\frac{8}{3} -\frac{8}{3} = \frac{8}{3}$

dilyakon

Математика

4,4(1 оценок)

10x/3=2/7 10x*7=3*2 70x=6 x=6/70

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.