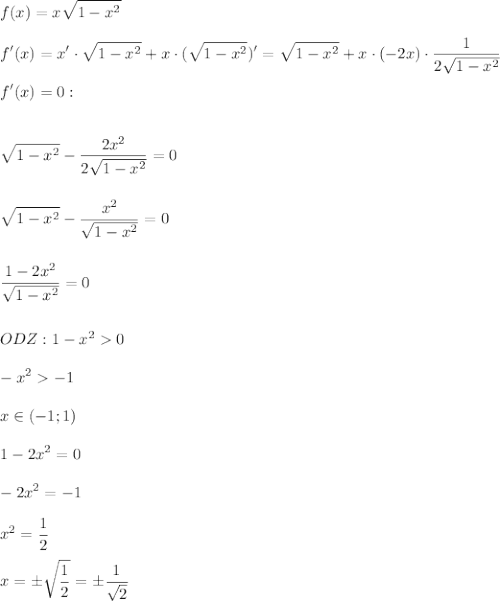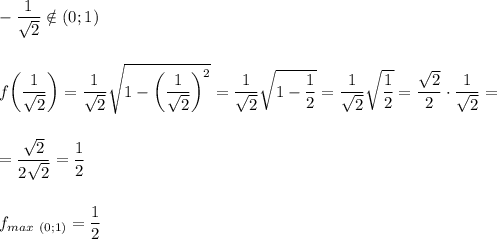Ответы на вопрос:
красивая-привлекательная
растопырить- раздвинуть
искаженный-испорченный
попятиться- отступить
Пошаговое объяснение:
синонимы- это слова, разные по написанию, но одинаковые по значению
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Выполни деление с остатком в столбик: 16 569 ÷ 27...
 Glebborg18.08.2022 16:20
Glebborg18.08.2022 16:20 -
576. Рациональные числа представьте в виде десятичных периодических...
 SlavaPogba25.02.2022 01:15
SlavaPogba25.02.2022 01:15 -
найдите координаты точки пересечения графика функции у равно 15 Икс...
 mozg3724.03.2023 16:36
mozg3724.03.2023 16:36 -
Определи недостающее значение при котором точка Т будет принадлежать...
 diana1515201.01.2023 03:20
diana1515201.01.2023 03:20 -
какое число задумано если задуманное число увеличили в 7 раз потом...
 катя1046774320.03.2022 13:41
катя1046774320.03.2022 13:41 -
6. Рациональные числа представьте в виде десятичных периодических...
 alisa284727417.05.2023 11:33
alisa284727417.05.2023 11:33 -
Нужно всё рассписать вот так: 3 1/15+ 2 7/25= (3+2)+(1/15 (доп. множитель...
 Аолвлвьвтадвлвл19.05.2023 02:34
Аолвлвьвтадвлвл19.05.2023 02:34 -
отрезки AB и CD пересекаются в точке О и делятся этой точкой пополам...
 вап2724.04.2020 00:42
вап2724.04.2020 00:42 -
Докажите что выражение 5 м - 1/3 м - 0,9 м + 0,4 не зависит от м...
 Soooooooonya02.11.2021 19:04
Soooooooonya02.11.2021 19:04 -
А^16*(а^6)^-3 при а= 1/9...
 poma07020503.10.2020 20:03
poma07020503.10.2020 20:03

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

 Найти наибольшее значение функции на интервале (0;1)
Найти наибольшее значение функции на интервале (0;1)