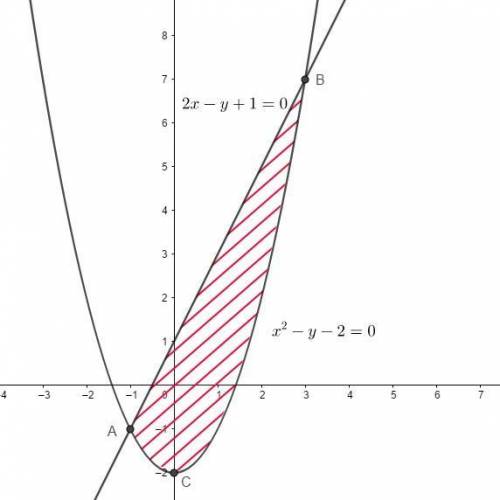
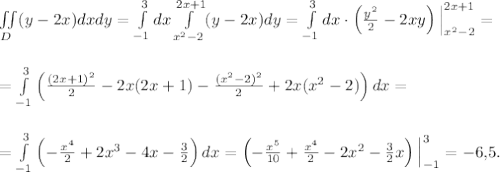tatyankasas

22.05.2021 18:10

Алгебра

Есть ответ 👍

Вычислить двойной интеграл по области , ограниченной указанными линиями.

218

365

Посмотреть ответы 2

Ответы на вопрос:

olmilevskaya1

Алгебра

4,4(72 оценок)

$\iint\limits_D(y-2x)dxdy=\int\limits^3_{-1}dx\int\limits^{2x+1}_{x^2-2}(y-2x)dy=\int\limits^3_{-1}dx\cdot \left(\frac{y^2}{2}-2xy\right)\Big|^{2x+1}_{x^2-2}=\\ \\ \\ =\int\limits^3_{-1}\left(\frac{(2x+1)^2}{2}-2x(2x+1)-\frac{(x^2-2)^2}{2}+2x(x^2-2)\right)dx=\\ \\ \\ =\int\limits^3_{-1}\left(-\frac{x^4}{2}+2x^3-4x-\frac{3}{2}\right)dx=\left(-\frac{x^5}{10}+\frac{x^4}{2}-2x^2-\frac{3}{2}x\right)\Big|^3_{-1}=-6{,}5.$

Вычислить двойной интеграл по области , ограниченной указанными линиями.

aliskaiii

Алгебра

4,4(2 оценок)

P = 2(a • b) - периметр прямоугольника.

р = а + b a полупериметр прямоугольника.

S = a•b ф площадь прямоугольника

По условию периметр Р = 200 м

Рассмотрим три варианта:

1) Участок квадратный.

Каждая сторона равна а.

Р = 4а

а = Р : 4

а = 200 : 4 = 50 м - длина стороны квадрата.

S = a • a

S = 50 • 50 = 2500 кв.м

2) Участок прямоугольный.

Предположим,

Р = 2•(70 + 30) = 200 м

Тогда

S = 70 • 30 = 2100 кв.м

3) Участок прямоугольный.

Предположим,

Р = 2•(90 + 10) = 200 м

Тогда

S = 90 • 10 = 900 кв.м

Видно, что наибольшую площадь 2500 кв.м имеет квадратный участок с длиной стороны 50 м.

ответ: участок квадратный; длина стороны 50 м, площадь участка 2500 кв.м.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.